Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Стехиометрия и энергетика метаболических превращений
Стехиометрия клеточного роста и образования продуктов метаболизма
Стехиометрия энергетического обмена; оценка количества выделяющейся теплоты и соответствующих экономических коэффициентов

В клетках химическая энергия используется очень эффективно, но, как и в любом другом реальном процессе, часть энергии субстрата выделяется в виде теплоты, что, в частности, обусловливает необходимость охлаждения биологических реакторов с культурами клеток. Клетки генерируют теплоту в первую очередь за счет процессов связанного с клеточным ростом метаболизма и энергообмена. Следовательно, можно предполагать наличие примерно пропорциональной зависимости между количеством выделившейся теплоты и количеством утилизированного высокоэнергетического субстрата. В этой связи был введен особый параметр — коэффициент Y_∆ (отношение количества образовавшейся клеточной массы в граммах к количеству выделившейся теплоты в килокалориях)» аналогичный рассмотренным выше другим экономическим коэффициентам. Если количество клеточной массы (в граммах), продуцируемой из одного грамма утилизированного субстрата, мы обозначим символом Y_s, а теплоты сгорания субстрата и клеточной массы (в килокалориях на грамм) — символами ∆H_s и ∆Н_с соответственно, то взаимосвязь между этими величинами будет выражаться следующим уравнением:

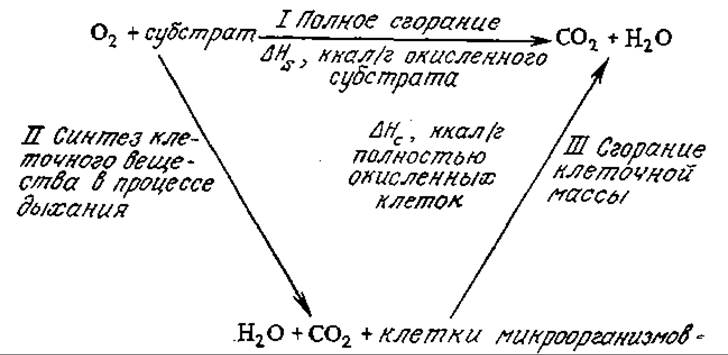
РИС. 5.30. Ориентировочный тепловой баланс утилизации субстрата.

Это уравнение вытекает из приближенного энергетического баланса между двумя путями полного окисления субстрата в случае аэробного роста, схематично изображенного па рис. 5.30.

Если окислителем в основном является кислород, то разность между количеством теплоты, выделяющейся при полном окислении одного грамма субстрата (∆H_S), и теплотой сгорания клеток (и сухого остатка внеклеточной жидкости), выросших на таком же количестве субстрата (Y_s∆H_c), будет приблизительно равна количеству теплоты, выделяющейся в процессе роста клеток (а также выделения Н₂О и СO₂) на одном грамме утилизированного субстрата.

Оценить точность допущений, положенных в основу уравнения (5.62) и схемы на рис. 5.30, можно на примере данных, относящихся к росту дрожжей на неразветвленных парафиновых углеводородах. Определенные экспериментальным путем величины ∆H_Sи ∆Н_с составляют 11,4 и 4,7 ккал/г соответственно; отсюда по уравнению (5.62) находим, что

Непосредственное измерение Y_Sи Y_∆ дало следующие результаты [16]:

В отсутствие экспериментальных данных теплоту сгорания клеток (как и любых других материалов) можно определить на основе следующего эмпирического факта. При переносе электронов от соединения СО степенью восстановленности y_s к соединениям е нулевой степенью восстановленности (например, СO₂ или Н₂O) выделяется количество энергии, равное K'∙y_s, где К — коэффициент, величина которого изменяется в пределах от 26 до 31 ккал на один химический эквивалент окисляемого вещества. Поскольку молекулярный кислород O₂ в процессе дыхания принимает четыре электрона, то поглощение моля кислорода должно сопровождаться выделением 104—124 ккал теплоты. На рис. 5.31 приведены экспериментальные данные для двух бактерий, дрожжей и плесени, выросших на различных средах. Разброс результатов довольно велик, но зависимость скорости тепловыделения от скорости поглощения кислорода просматривается достаточно отчетливо.

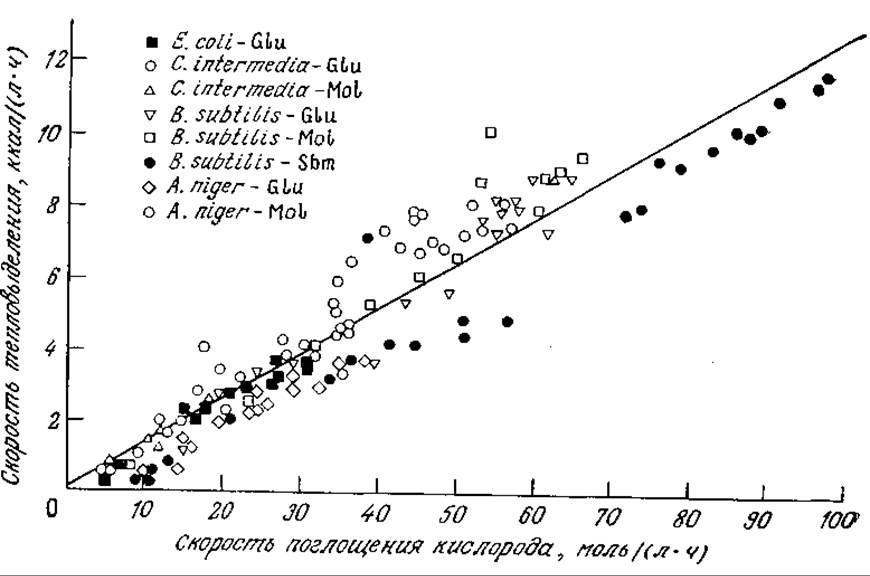
РИС. 5.31. Экспериментально найденные скорости тепловыделения и поглощения кислорода в процессе роста ряда микроорганизмов в различных средах (Glu — глюкозная среда, Mol — среда на основе мелассы, Sbm — среда на основе соевых бобов). Наклон прямой регрессионной зависимости равен 124±3 ккал/моль O₂. [Воспроизведено с разрешения из работы: Cooney С. L, Wang D. I. С., Mateles R. I., Measurement of Heat Evolution and Correlation with Oxygen Consumption during Microbial Growth, Biotech. Bioeng., 11, 269 (1968)].

В качестве примера оценим теплоту сгорания клеток Pseudomonas fluorescens, растущих на глюкозной среде. Для этого прежде всего запишем уравнение реакции сгорания клеток в расчете на экспериментально найденную «брутто-формулу», приняв, что продуктами сгорания являются СO₂, Н₂O и N₂:

Далее определим теплоту, выделяющуюся при сгорании бактерий по уравнению (5.63), приняв теплоту сгорания в расчете на 1 моль O₂ равной 104 ккал:

При этом¹ мы не учли, однако, что сухое вещество клеток содержит и золу. Если в сухом клеточном веществе содержится 10% золы, то теплота сгорания клеток будет равна

Таблица 5.12. Экономические коэффициенты для бактерий, растущих на средах с различными источниками

^а Из работы. Abbott В. Clamen A., The Relationship of Substrate, Growth Rate, and Maintenance Coefficient to Single Cell Protein Production, Biotech. Bioeng., 15, 117 (1973).

Значение Y_∆ зависит от природы как микроорганизма (влияющего на ∆Н_С), так и утилизируемого субстрата (влияющего на ∆H_s). В табл. 5.12 приведен ряд вычисленных значений коэффициентов Y_∆ в зависимости от природы субстрата. Обратите внимание на то, что в общем случае углеводороды обеспечивают большее тепловыделение, чем частично окисленные соединения [Y_∆(СН₄) < Y_∆(СН₃ОН); Y_∆(н-алканы) < Y_∆(глюкоза)]. Следовательно, более восстановленные субстраты в большей степени требуют отвода тепла от биореактора. Влияние энергетической стехиометрии на экономику процессов рассмотрено в гл. 12.

В процессах брожения или очистки сточных вод субстратами часто являются смеси множества веществ с различными теплотами сгорания. Сервици и Боуген [18] отметили, что стехиометрическое отношение m₀ (число молей O₂, необходимого для полного окисления 1 моль субстрата) для ряда соединений пропорционально стандартной свободной энергии сгорания ∆G°. Например, для углеводов, промежуточных соединений цикла ТКК и некоторых продуктов гликолиза

∆G°= - 116m₀ ккал/моль субстрата      (5.66)

а для ароматических соединений, спиртов и алифатических кислот

∆G°= - 104m₀ ккал/моль субстрата      (5.67)

[Хаттори (ссылка [4] в гл. 13) отмечал, что если известна величина химической потребности в кислороде (ХПК), выраженная в граммах кислорода на моль, то вместо m₀ в этих уравнениях можно применять ХПК/32.] Усредненную свободную энергию полного окисления смеси субстратов можно определить суммированием свободных энергий окисления всех индивидуальных субстратов:

где і — субстраты; М_i — число молей і-го субстрата; ∆G_i° — свободная энергия полного окисления і-го субстрата.

Оказалось также, что экономический коэффициент У процесса, в котором участвуют несколько видов одноклеточных организмов, можно определить так же, как и в случае описанных выше процессов с участием микроорганизмов одного вида (бактерий или дрожжей). Сервици и Боуген [18] определили средние экономические коэффициенты (выраженные в граммах клеток на моль субстрата) для активного ила (см. гл. 14), содержащего множество микроорганизмов и большое число субстратов, и нашли (рис. 5.32), что

При данном Y_s все других величины, входящие в уравнение (5.62), легко определить экспериментально; следовательно, и в этом случае можно вычислить Y_∆.

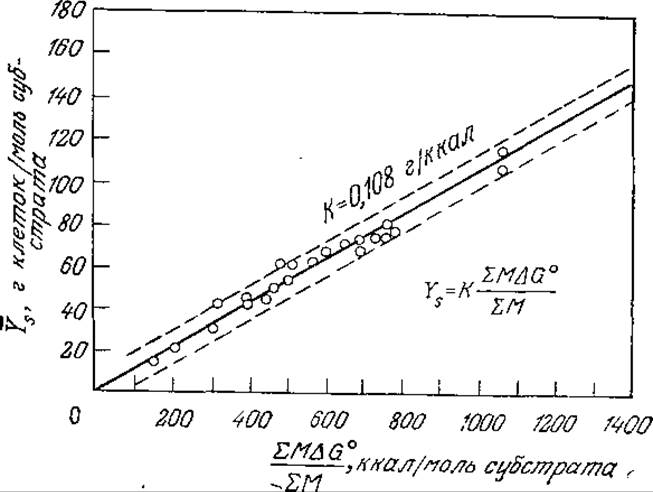
РИС. 5.32. Зависимость среднего экономического коэффициента роста активного ила от средней свободной энергии окисления субстратов. [Воспроизведено из работы: Seruizi J. A., Bogan R. Н., Thermodynamic Aspects of Biological Oxydation and Synthesis, J. Water Pollut. Control Fed., 36, 607 (1961).]

Следует ожидать, что величина коэффициента в уравнении (5.69) зависит от вида микроорганизма, поэтому опять-таки желательно экспериментальное определение этого коэффициента по отношению к участвующему в процессе организму (или организмам). В то же время, предполагая существование пропорциональной зависимости между

Cервици и Боуген исходили из линейной зависимости между средним экономическим коэффициентом и числом NATP молекул АТР, синтезируемых в ходе утилизации 1 моль субстрата. Поскольку есть не что иное, как количество клеток (в граммах), синтезируемых из 1 г субстрата, то коэффициент пропорциональности между и АTP представляет собой массу клеток (в граммах), синтезируемых в процессе утилизации 1 моль АТР. Известно, что последняя величина приблизительно постоянна для большого числа анаэробов, но изменяется в гораздо более широких пределах в случае аэробных организмов (разд. 5.9.2). В отсутствие более надежных данных уравнение (5.69) в общем случае может служить основой для оценки систем, состоящих из нескольких субстратов и микроорганизмов. Точность такой оценки, по-видимому, не превышает ±20—30%, о чем наглядно-свидетельствуют корреляционные данные, приведенные на рис. 5.32.

Упоминавшаяся выше взаимосвязь между числом участвующих в процессе электронов и внутренней энергией вещества может быть использована для оценки максимально возможного выхода органического вещества из органического субстрата. Долю электронов, переходящих в процессе реакции от субстрата к продуктам метаболизма, ζ_p можно определить по уравнению

Последний член правой части уравнения (5.70) представляет собой экономический коэффициент Y_P/S. Число участвующих в процессе электронов в 1 г органического вещества можно выразить как σу/12, где а — массовая доля углерода в соединении и у — степень восстановленности этого углерода. Подставив это выражение в уравнение (5.70), получим

Поскольку энергии субстрата и продукта метаболизма приблизительно пропорциональны содержанию в них участвующих в реакции электронов, то параметр ζ_р можно интерпретировать и как энергетический коэффициент выхода продукта метаболизма из субстрата. В этом случае, очевидно, коэффициент не должен превышать единицы. Следовательно, верхний предел выхода продукта метаболизма Y_p/s^max можно определить по уравнению (5.71) при ζ_р = 1:

Значения Y_p/s^max для нескольких субстратов и продуктов метаболизма приведены в табл. 5.13.