Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989
Кинетика процессов утилизации субстрата, образования продуктов метаболизма и биомассы в культурах клеток
Кинетика клеточного роста в переходном состоянии
Неструктурированные модели клеточного роста в периодических процессах
В простейшем подходе к моделированию роста культуры клеток в периодическом процессе мы допускаем, что скорость роста клеточной массы во времени является функцией одной лишь клеточной массы, т. е.
![]()
Как мы скоро увидим, из этого уравнения отнюдь не следует, что мы должны пренебрегать любыми изменениями, происходящими в ходе клеточного роста в среде.
Одной из простейших моделей типа (7.49) является закон Мальтуса, который математически можно выразить следующим образом:
f(x) = μx (7.50)
где μ — константа. Нетрудно видеть, что таким же образом выражается уже известная нам закономерность накопления клеточной массы в фазе экспоненциального роста. Предсказание Мальтуса о неизбежности рокового конца человечества в результате неконтролируемого роста народонаселения не оправдалось (или, быть может, пока еще не оправдалось?); так же и в случае популяций микроорганизмов вслед за фазой экспоненциального роста наблюдается переход к стационарной популяции.
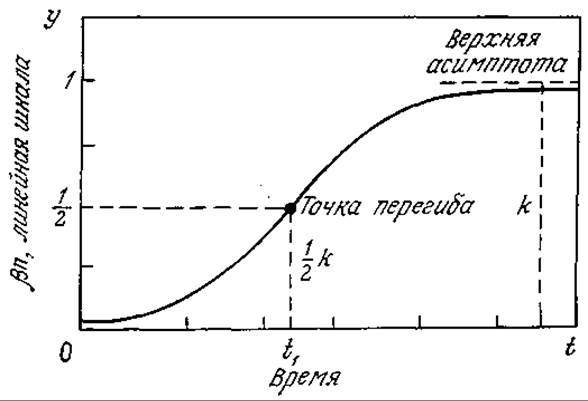
РИС. 7.19. Логистическая кривая (ß > 0; ß > 0).
Эта теория получила дальнейшее развитие в работах Ферлхурста (1844 г.), а также Перла и Рида (1920 г.), которые при анализе роста популяции стали учитывать ингибирующий фактор. Допустив, что ингибирование пропорционально х2, эти исследователи предложили уравнение
![]()
Это выражение представляет собой уравнение Риккати; его интегрирование не представляет затруднений и приводит к уравнению логистической кривой:
![]()
Как показано на рис. 7.19, логистическая кривая имеет S-образную форму и приводит к стационарной популяции с максимальной концентрацией биомассы xs = 1/ß.
Одно из возможных объяснений логистической кривой сводится к допущению, что скорость продуцирования токсина про-
порциональна скорости роста популяции:
![]()
И если
сt( 0) = 0 (7.54)
то
ct = а(х — х0) (7.55)
Обычно х0 пренебрежимо мало по сравнению с х; в таких случаях подстановка уравнения (7.55) в (7.42) приводит к уравнению типа (7.51).
В основу неструктурированных моделей другого типа, описывающих приближающиеся к стационарному состоянию популяции, положен принцип истощения лимитирующего рост питательного вещества. Если, как и при выводе уравнения Моно, допустить, что μ = μ(s) и что общий экономический коэффициент Yх/s постоянен, то уравнения материального баланса для питательного вещества и клеточных веществ можно объединить в одном уравнении типа (7.49) (см. упражнение 7.14).
Недостатком логистического уравнения является пренебрежение фазой снижения массы (численности) популяции после того, как стационарная популяция исчерпала все свои ресурсы. Этот фактор учтен в модели, разработанной в начале этого столетия Вольтеррой. В модели Вольтерры уравнение (7.50) дополняется интегральным членом типа
![]()
Физический смысл выражения (7.56) в первом приближении можно интерпретировать как влияние истории популяции K(t,r) на скорость ее роста. Выражение (7.56) отражает зависимость скорости роста во-время t от всех предыдущих значений плотности популяции. Если К не зависит от t, то выражение (7.56) можно рассматривать как отражение влияния компонента культуры, изменение концентрации которого подчиняется закону
![]()
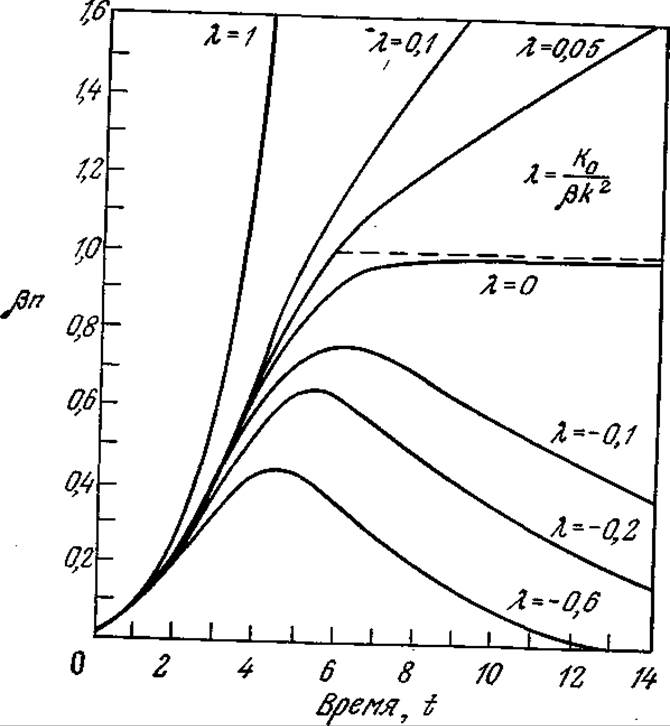
РИС. 7.20. Решение уравнения Вольтерры при различных значениях параметра λ, отражающего историю популяции клеток,
Предположим, что К постоянно и равно К0, и дополним уравнение (7.51) выражением (7.57), отражающим предыдущую историю популяции. Тогда изменение массы или плотности популяции во времени можно описать следующим уравнением
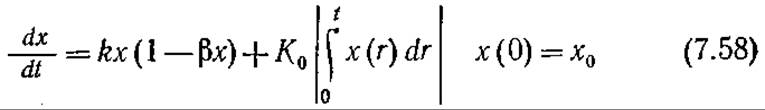
В соответствии с уравнением (7.58) Ко для ингибитора имеет отрицательное значение, а для соединения, промотирующего клеточный рост, — положительное. Это уравнение можно решить численно; пример такого решения приведен на рис. 7.20. При отрицательных К0 масса популяции достигает максимума и затем уменьшается.
Описанные выше неструктурированные модели клеточного роста имеют несколько недостатков. В частности, в них не находит отражения лаг-фаза, не учтены влияющие на рост клеток различные переменные, а также данные о метаболизме клетки и его регуляции. В последующих разделах мы попытаемся найти связи между сложной биохимией клетки и явлениями, наблюдаемыми при росте популяции в периодическом процессе.