Химия белка. Структура, свойства, методы исследования - Шендрик А.Н. 2022
Методы экспериментального исследования структуры белков
Рентгеноструктурный анализ
Особенности РСА белков
Установить структуру методом РСА - означает восстановить по картине рефлексов в обратном пространстве, исходную кристаллическую решетку, породившую эту картину, в реальном пространстве самого кристалла. Решение этой задачи всегда представляло серьезные трудности даже для простых молекул. При переходе же к биологическим объектам потребовались просто нетрадиционные или специфические приемы проведения РСА.
Основное, что было разработано Кембриджской школой (Перутц, Кендрю) в приложении к РСА белков - это экспериментальный метод определения фаз. Как это удалось?
Макромолекулы белков образуют молекулярную решетку, в которой они уложены рядом друг с другом. На модели (см. рис.4.20) приведена упаковка молекул миоглобина в решетке. Кристаллическая решетка моноклинная, и в элементарную ячейку входят 2 макромолекулы. Сама по себе внутримолекулярная структура миоглобина чрезвычайно сложна, но способ упаковки целых макромолекул в решетке прост. Между макромолекулами столь замысловатой формы с необходимостью должны оставаться зазоры, заполняющиеся при кристаллизации белка водным раствором. Кристаллизационная вода заполняет в белковых кристаллах часто половину и даже несколько большую часть всего объема. Высушивание белкового кристалла вызывает обычно нарушение регулярности структуры. Напомним, что белковые кристаллы долгое время вообще не считали за кристаллы, так как они не давали рентгеновской дифракции. Бернал и Дороги Ходжкин показали, что ошибка была в высушивании кристаллов; если снимать рентгенограмму с белкового кристалла, находящегося в маточном растворе, удается получить поразительные по детальности рентгенограммы, насчитывающие часто более 20000 независимых рефлексов (см. рис. 4.21).
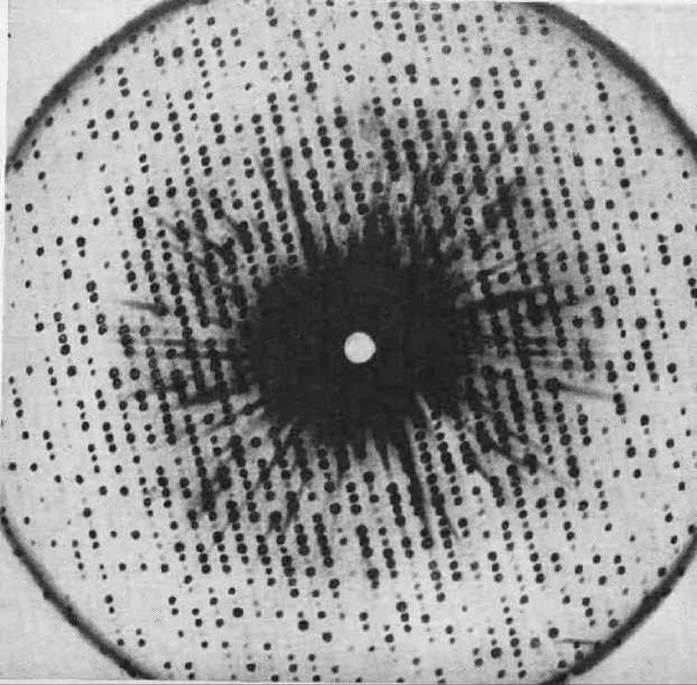
Рис. 4.21 Рентгеновская дифрактограмма от кристалла гемоглобина
Предположим теперь, что мы вводим в каждую макромолекулу белка (будем рассматривать для конкретности гемоглобин) тяжелый атом с высоким атомным номером и притом вводим закономерно, т. е. путем химической реакции с какой-то строго определенной функциональной группой. Еще одно необходимое требование заключается в том, что результирующее соединение белка с тяжелым атомом должно быть изоморфно с исходным белком, т. е. кристаллизоваться в той же решетке. Если эти условия выполнены, то тяжелые атомы в основном изменяют интенсивности отдельных пятен в рентгенограмме, не меняя рентгенограмму коренным образом. Простейшим примером вполне приемлемых для этих целей тяжелых атомов являются атомы ртути. Они обладают специфическим сродством к сульфгидрильным группам. Вводя в маточный раствор, из которого ведется кристаллизация гемоглобина, специфический ртутный реактив парахлормеркурибензоат натрия можно получить белок, в котором две сульфгидрильные группы на каждую макромолекулу прореагировали с ртутным соединением.
![]()
Таким образом в каждой элементарной ячейке кристалла в определенных точках будут находиться четыре атома ртути, сильно рассеивающие рентгеновские лучи. Сняв картину дифракционных пятен от кристалла ртутного соединения и сопоставляя ее с соответствующими данными для незамещенного белка, мы получим картину рентгеновской дифракции от пространственной решетки, состоящей как бы из одних атомов ртути, расставленных в пространстве в точках, где эти атомы прикрепляются благодаря химическому взаимодействию с белком. Решетка атомов ртути, естественно, имеет простую структуру (всего 4 атома ртути в элементарное ячейке).
Определение дифракционной картины для разностной “ртутной” решетки представляется непростым делом. Нельзя обойтись простым вычитанием интенсивностей пятен комбинированной рентгенограммы белок ртуть и рентгенограммы чистого белка. Складываются не интенсивности (квадраты амплитудных коэффициентов), а сами амплитудные коэффициенты. Последние, как уже сказано выше, определяются модулем и фазой. Это комплексные числа и они складываются как векторы на плоскости. А решение фазовой задачи сводится к совместному решению векторных уравнений, полученных для нескольких различных соединений тяжелого атома с белком. Большую помощь при этом оказывают двойные дериваты, содержащие два разных тяжелых атома в двух точках макромолекулы. Большое облегчение в структурном анализе оказывает наличие оси симметрии кристалла 2-го порядка.
Не останавливаясь на деталях, отметим, что “ртутная” решетка, хотя ее элементарная ячейка остается моноклинной, все же примитивна, так как содержит в каждой ячейке немного атомов. Поэтому ее полный рентгеноструктурный анализ осуществляется относительно просто и без принципиальных затруднений. А тогда оказывается возможным вычислить ретроспективно значения всех амплитудных коэффициентов, причем вычислить их полностью, т. е. определить амплитуды и фазы. Знание всей пространственной картины как в прямом, так и в обратном пространстве для “ртутной” решетки используется для решения основной задачи - нахождения фаз амплитудных коэффициентов для кристалла белка.
Для самоконтроля рентгенографисты стремятся иметь не 2 замещенных тяжелыми атомами изоморфных белковых деривата, а 4 - 5 и более. Тогда степень надежности и точности в определении фазы для каждого дифракционного пятна возрастает в большей мере и всякая случайная ошибка вскрывается, так как приводит к несогласованности данных.
Из всего сказанного можно лишь в общих чертах представить себе колоссальный объем измерений и вычислений. Зато после определения фаз и суммирования рядов Фурье мы имеем все, т. е. значения электронной плотности p(x,y,z) в каждой точке пространства внутри элементарной ячейки. Точки, где электронная плотность проходит через максимум, дают нам координаты атомов.
Чтобы построить с помощью электронной плотности пространственную модель молекулы, ее восстанавливают по слоям. Все это напоминает систему гистологических срезов через сложную ткань, когда накладывая друг на друга последовательные срезы, мы реконструируем пространственную картину ткани. Подобным же образом реконструируют пространственную картину молекулы по плоским срезам поверхностей равной электронной плотности (см. рис. 4.22).
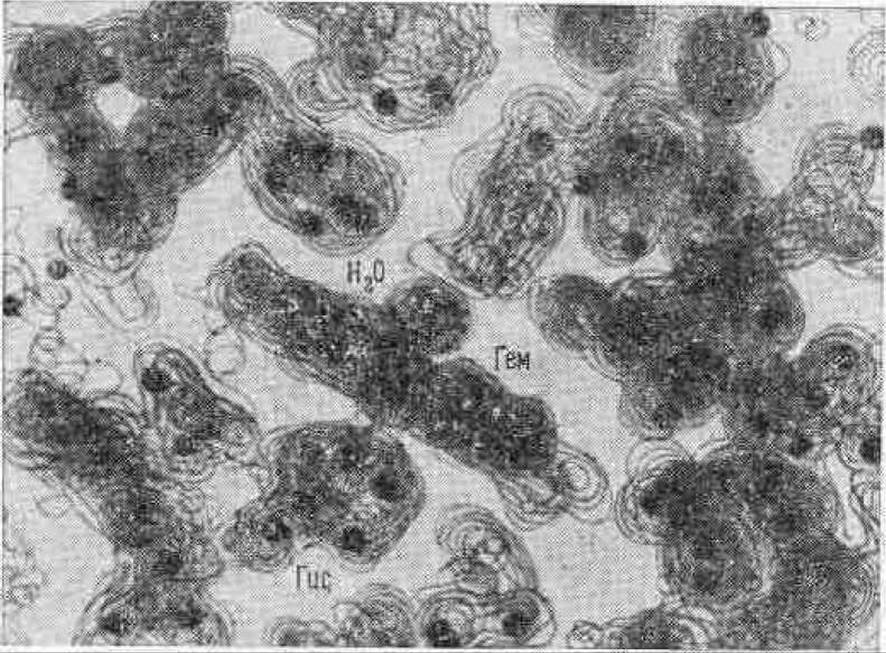
Рис. 4.22 Пространственное распределение электронной плотности в миоглобине.
Для иллюстрации идеи изоморфного замещения для решения фазовой проблемы при РСА сложных молекул Бреггом был предложен простой и весьма оригинальный эксперимент. В нем, вместо дифракции рентгеновских лучей Брэгг предложил наблюдать дифракцию видимого света, вместо пространственной решетки - плоскую решетку. Чтобы осуществить дифракцию видимых лучей, пользуются простым прибором, изображенным на рис. Свет от источника А собирается конденсором в главном фокусе плоско-выпуклой линзы. Затем параллельные лучи проходят через маску О. Это черная бумага, в которой пробиты отверстия.
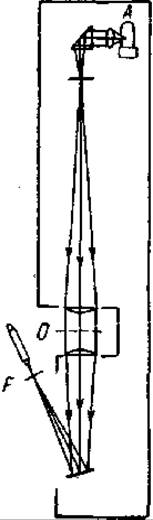

Рис. 4.23 Маска, моделирующая одну (А) и две (Б) и четыре молекулы гексаметилбензола (левая часть рисунка). Те же маски с одним дополнительным отверстием в центре (правая часть рисунка)
Расположение дырочек соответствует расположению атомов в изучаемой молекуле. Например, на рис.4.23 изображена маска, передающая строение гексаметилбензола (напоминаем, что атомы водорода в РСА могут не приниматься во внимание). После второй линзы лучи фокусируются в плоскости F, в которой и образуется дифракционная картина. Она рассматривается через микроскоп малого увеличения. Вот и весь прибор для визуального наблюдения дифракции света.
На рис. 4.23 (левая часть) изображены дифракционные картины, полученная от масок моделирующих одну, две и четыре правильно расположенные на плоскости молекулы гексаметилбензола. Видно, что уже одна молекула дает систему дифракционных пятен, общее расположение которых сохраняется и для решетки из нескольких молекул. Но каждое пятно дробится на несколько и получается в конечном счете сложная картина, в которой межмолекулярные и внутримолекулярные интерференции перемешаны.
Спрашивается, можно ли, зная дифракционную картину, получить расчетом или измерением породившую ее картину дырочек или освещенных точек. Оказывается, это было бы возможно и легко, если бы мы знали не только амплитуды (их квадрат - интенсивность пятна), но и фазы колебаний в дифракционных пятнах. В данном случае мы имеем дело с картиной в прямом пространстве гораздо более элементарной, чем белковый кристалл. Эта картина плоская, с центром симметрии. При этом все фазы интерференции имеют только два значения: 0 и п. Иначе говоря, неопределенность фазы пятен сводится к неопределенности знаков амплитудных коэффициентов, т.е "+" или "-". Если бы мы знали знаки, соответствующие каждому из пятен, т. е. каждой точке в обратном пространстве, не представляло бы труда реконструировать (рассчитать через ряды Фурье) структуру “кристаллической ячейки гексаметилбензола”, исходя из дифракционной картины. Поскольку знаки амплитудных коэффициентов неизвестны - вычислить ряды Фурье нельзя. Существенно, однако, то, что можно обойтись без расчетов, а пойти путем аналогового решения задачи, т.е. применить тот же прием дифракции видимого света для преобразования картины пятен из обратного пространства в прямое. Для этого нужно изготовить маску с дырочками, соответствующими дифракционной картине (рис. 4.23 левая часть). Но этого недостаточно. Часть дырочек должна давать пучок света с обратной фазой колебаний по отношению к остальным и расположение этих дырочек надо знать. Зная эти отверстия, мы заклеиваем их прозрачной слюдяной пластинкой, дающей запаздывание по фазе точно на п (толщина пластинки подбирается равной половине длины волны света в данной среде). Тогда мы получаем в фокусной плоскости нашей оптической системы картину расположения атомов в “молекулах” гексаметилбензола.
Таким образом, обратная задача перехода от дифракционной картины к “структуре решетки” решается аналоговым путем только в том случае, если известны фазы (в данном случае знаки) интерференционных максимумов. Фазы заранее неизвестны (мы видим и измеряем на практике только интенсивность пятен), поэтому необходимо прибегнуть к методу изоморфного замещения. Для этого вводим в структуру “молекулы” лишнюю освещенную точку в определенном месте. Для простоты в нашем примере лишняя дырочка в маске сделана в самом центре (рис. 4.23, правая часть). Получаем дифракционные картины от измененных “молекул” и сравниваем их с дифракционными картинами от первоначальных “молекул”. Поскольку здесь дело гораздо проще и необходимо выбрать только между двумя фазами - 0 и п, качественное сравнение двух картин вполне достаточно и дает сразу же полный ответ на поставленный вопрос. Действительно, дополнительная дырочка находится в центре симметрии “молекулы”. Анализ показывает, что все амплитудные коэффициенты, создаваемые этими центральными дырочками, будут иметь знак плюс. Значит, если дифракционное пятно увеличило свою интенсивность после добавления центрального “атома” в “молекуле” гексаметилбензола, то его амплитудный коэффициент положителен, если же уменьшило, то отрицателен.
Сравнивая левые и правые стороны рис. 4.23, мы легко находим пятна с положительными и отрицательными знаками амплитудных коэффициентов. В этом и заключена, правда с большими упрощениями, основная физическая идея метода изоморфного замещения. При анализе белковых кристаллов дело обстоит несравненно сложнее и вот по каким причинам.
Во-первых, решетка пространственная; во-вторых, центр симметрии отсутствует (в белках не может быть центра симметрии хотя бы уже потому, что они содержат асимметрические атомы углерода). Но в принципе брэгговская иллюстрация помогает понять саму идею метода.
Возвращаясь к рентгеноструктурному анализу белков, рассмотрим, имеющий теперь уже только исторический интерес, путь пройденный при РСА исследовании миоглобина. Характерными являются несколько последовательных этапов, проделанных в этой работе. Разрешающая способность метода рентгеноструктурного анализа находится в известной мере во власти исследователя. В начале было решено ограничиться более грубой картиной, пренебрегая мелкими деталями. Было принято, что анализ ведется с разрешением в 6 Å. Это означало, что интерференции, соответствующие расстояниям в прямой решетке меньше 6 Å, во внимание не принимались. В этом случае, в обратном пространстве выбрасываются все пятна, расстояния которых от центра больше определенного. Иначе говоря, выбор разрешающей силы приводит к тому, что мы отбираем дифракционные максимумы, достаточно близкие к центральному пятну, и тем ограничиваем используемый экспериментальный материал. Так, для получения пространственной модели миоглобина с разрешением в 6 Å оказалось необходимым использовать 400 дифракционных пятен. При переходе к разрешению в 2 Å объем обратного пространства, который приходится использовать для анализа, возрастает в 33 = 27 раз. Отсюда число дифракционных пятен, использованных для расчетов, составило 10 000. При повышении разрешения до 1,5 Å объем обратного пространства и, соответственно, число дифракционных максимумов возросло еще вдвое, т. е. для анализа служили 20000 интерференционных пятен.
Картина, полученная при разрешении в 6 Å, не позволила выявить положение отдельных атомов, но положение спиралей Полинга - Кори, образованных полипептидной цепью, было установлено четко, так как диаметр спирали 10,1 Å. Боковые цепи аминокислотных звеньев здесь получились как бесструктурная аморфная масса, заполняющая промежутки между стержнеобразной спиралью. По причине того, что отдельные белковые группы идентифицировать не удалось, о чередовании аминокислот в цепи ничего сказать было нельзя. Следующим шагом было повышение разрешающей способности до 2 Å путем анализа 9600 интерференций. Такую титаническую работу можно было осуществить только путем значительной механизации, в особенности всех численных расчетов. Кристаллики миоглобина (из мышц кашалота) снимались для получения так называемых диаграмм колебаний из 22 различных положений. Затем после фотометрирования всех пятен проводилась нормировка интенсивностей всех отдельных рентгенограмм c тем, чтобы получить вполне сравнимую серию из 9600 коэффициентов. Затем вся та же измерительная работа была проделана на четырех изоморфных дериватах белка, содержащих тяжелые атомы металлов.
К счастью, оказалось, что подобные дериваты образуются довольно легко и в значительном разнообразии. В состав белковой молекулы входят многие активные функциональные группы, способные связывать атомы или ионы металлов как ковалентно, так и путем комплексообразования. Для надежности следует выбирать такие соединения, для которых число связанных атомов металлов на одну молекулу белка невелико (лучше всего 1 - 2). Необходимо, чтобы положение тяжелых атомов было строго фиксировано в определенных точках макромолекулы, но знать заранее координаты этих точек нет необходимости. Наконец, обязательным является изоморфизм белкового деривата с исходным белком. Это требование, как правило, нетрудно выполнить: введение одной или двух групп с тяжелым металлом в макромолекулу белка зачастую почти не изменяет упаковку макромолекул в элементарной ячейке (решетке). Во всяком случае, возникающие деформации решетки оказываются пренебрежимо малы. Все эти обстоятельства помогают решить химическую часть задачи - получение дериватов белков с атомами тяжелых элементов, причем критерием образования нужных соединений служат обычно сами рентгенограммы соответствующих кристаллов.
Применительно к миоглобину лучшими реагентами оказались следующие. Первый - это парахлормеркурибензосульфонат.
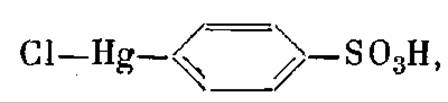
Это вещество присоединяется в одном единственном месте, даже если задать его в кристаллизационную жидкость в 20-кратном избытке.
Второй реагент - комплексные ртутно-аммиачные ионы, образующиеся при нагревании окиси ртути с водным аммонийсульфатом. Эти ионы присоединяются к молекуле миоглобина также в одном единственном месте и притом в совершенно другом, чем первое, ртутно-органическое соединение. Третий, пригодный для рентгеноструктурного анализа, дериват содержал комплексный ион золота AuCl4- (добавлялась при кристаллизации миоглобина соль KAuCl4). Золото прикрепляется также в одной определенной точке макромолекулы миоглобина. Реакция идет очень медленно и требует нескольких месяцев. Четвертое соединение содержало в комбинации ртуть в виде хлормеркурибензосульфоната и ртутно-аммиачного комплекса.
Для всех четырех дериватов были получены рентгенограммы также из 22 положений и точно измерены около 10000 дифракционных максимумов. Затем были получены разностные картины, относящиеся к атому тяжелого металла, вычислены координаты атома металла, получены для него амплитудные коэффициенты как по величине, так и по фазе. Наконец, решением векторных уравнений получены фазы всех 9600 интерференции миоглобина, и в итоге проведено суммирование рядов Фурье для 96 слоев, на основании чего построены поверхности равной электронной плотности. Степень выразительности этой картины такова, что вторичная и третичная структура белка получилась во всех деталях, структура спиральных участков Полинга - Кори подтвердилась в полной мере. Степень спиральности миоглобина оказалась близкой к 77%, что хорошо совпадало с оценкой, сделанной Бенсоном и Линдерштрём - Лангом на основании изотопного обмена водорода пептидных связей. Природа боковых радикалов аминокислот в этом приближении установлена в большинстве случаев, но не во всех. Только в следующем окончательном расчете с разрешением в 1,5 Ä, когда приходится иметь дело с 20000 дифракционных пятен, степень детальности анализа оказалась такой, что удалось идентифицировать все аминокислотные остатки.