БИОХИМИЯ - Л. Страйер - 1984

ТОМ 2

ЧАСТЬ II ГЕНЕРИРОВАНИЕ И ХРАНЕНИЕ МЕТАБОЛИЧЕСКОЙ ЭНЕРГИИ

ГЛАВА 11 МЕТАБОЛИЗМ: ОСНОВНЫЕ ПОЛОЖЕНИЯ И ОБОЗНАЧЕНИЯ

11.1. Свободная энергия - самая полезная термодинамическая функция в биохимии

Сначала вспомним некоторые положения термодинамики, имеющие важное значение для понимания процессов обмена веществ. В термодинамике система-это совокупность предметов внутри определенной области. Все остающееся за пределами этой области и находящееся в остальной части пространства обозначается как окружающая среда. Первый закон термодинамики гласит, что общая энергия системы и окружающей среды-величина постоянная. Иными словами, энергия сохраняется. Математическое выражение первого закона термодинамики имеет следующий вид:

∆E = Е_в-Е_А = Q-W, (1)

где E_A-энергия системы в начале процесса, а E_в-энергия в конце процесса; Q-тепло, поглощаемое системой; W-работа, совершаемая системой. В уравнении (1) следует обратить внимание на тот важный факт, что изменение энергии системы зависит только от начального и конечного состояний и не зависит от пути превращения.

Рис. 11.1. Примеры процессов, которые индуцируются при повышении энтропии системы: A-диффузия тепла; Б-диффузия растворенных веществ

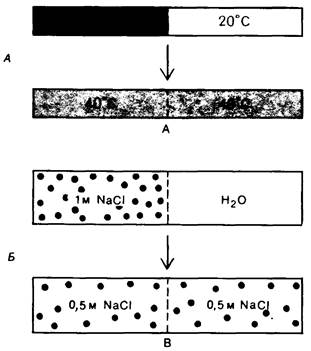
Первый закон термодинамики не дает возможности предсказать, может ли та или иная реакция протекать спонтанно. Некоторые реакции все же идут спонтанно, несмотря на положительное значение ∆E. При этом система поглощает тепло из окружающей среды, так что суммарная энергия системы и окружающей среды остается постоянной. Очевидно, в этих случаях для предсказания спонтанности процесса требуется функция, отличная от ∆E. Одной из таких функций является энтропия (5), которая служит мерой степени беспорядочности или разупорядоченности системы. Энтропия системы возрастает (∆S имеет положительное значение), когда увеличивается степень разупорядоченности. Второй закон термодинамики гласит, что процесс может протекать спонтанно только при условии увеличения суммы энтропий системы и окружающей среды

(∆S_{cистемы} +∆S_среды) > 0 для спонтанного процесса. (2)

Следует обратить внимание на следующий факт: во время спонтанного процесса энтропия системы может уменьшаться при условии, что энтропия окружающей среды увеличивается, так что их сумма оказывается положительной величиной. Например, образование высокоупорядоченной биологической структуры термодинамически возможно, поскольку снижение энтропии в такой системе более чем возмещается повышением энтропии окружающей среды.

Одна из трудностей использования энтропии в качестве критерия возможности спонтанного протекания биохимического процесса состоит в том, что изменения энтропии при химических реакциях измерить нелегко. Кроме того, критерий спонтанности, даваемый уравнением (2), требует, чтобы было известно изменение энтропии и окружающей среды и исследуемой системы. Эти трудности устраняются при использовании другой термодинамической функции, называемой свободной энергией, которая обозначается символом G (или F в более ранних источниках). В 1878 г. Джошуа Виллард Гиббс (Josiah Willard Gibbs) построил функцию свободной энергии путем сочетания первого и второго законов термодинамики. Основное уравнение при этом следующее:

∆G = ∆Н - T∆S, (3)

где ∆G-изменение свободной энергии системы, претерпевающей трансформацию при постоянных давлении (Р) и температуре (Т), ∆Н-изменение энтальпии системы, a ∆S-изменение энтропии этой системы. Следует отметить, что никакие параметры окружающей среды не входят в это уравнение. Изменение энтальпии вычисляется из уравнения

∆Н = ∆Е + P∆V; (4)

Изменение объема А V мало почти для всех биохимических реакций, а это значит, что ∆Н почти равно ∆Е. Отсюда

∆G - ∆E - T∆S. (5)

Таким образом, ∆G реакции зависит как от изменения внутренней энергии, так и от изменения энтропии системы.

Изменение свободной энергии (∆G) реакции в отличие от изменения внутренней энергии (∆Е) служит ценным критерием возможности спонтанного протекания этой реакции.

1. Реакция может идти спонтанно только при отрицательном значении ∆G.

2. Система находится в равновесии и не претерпевает никаких изменений, когда ∆G равно нулю.

3. Реакция не может идти спонтанно при положительном значении ∆G. Для индукции такой реакции требуется приток свободной энергии.

Здесь необходимо подчеркнуть еще два дополнительных момента. Во-первых, ∆G реакции зависит только от разности: свободная энергия продуктов (конечное состояние) минус свободная энергия реагирующих веществ (начальное состояние). ∆G реакции не зависит от пути превращения. Механизм реакции не оказывает влияния на ∆G. Например, значение ∆G для окисления глюкозы до СO₂ и Н_2O остается одним и тем же вне зависимости от того, осуществляется ли это превращение путем сгорания in vitro или же в результате серии многих ферментативных реакций в клетке. Во-вторых, ∆G не дает информации о скорости реакции. Отрицательное значение ∆G указывает, что данная реакция может протекать спонтанно, однако это еще не значит, что она будет идти с заметной скоростью. Как обсуждалось ранее (разд. 6.6), скорость реакции зависит от свободной энергии активации (∆G⁺), которая не связана с ∆G.

Единицы энергии -

Калория (кал) эквивалентна такому количеству тепла, которое требуется для повышения температуры I г воды с 14,5 до 15,5 С.

Килокалория (ккал) равна 1000 кал.

Джоуль (Дж)-количество энергии, необходимое для приложения силы в 1 Н па расстоянии 1 м.

Килоджоуль (кДж) равен 1000 Дж.

1 ккал = 4,184 кДж.

11.2. Изменение стандартной свободной энергии реакции и его связь с константой равновесия

Рассмотрим реакцию А + В ⇄ C + D.

∆G этой реакции дается уравнением

(6)

где ∆G⁰-изменение стандартной свободной энергии, R-газовая постоянная, Т- абсолютная температура, [А], [В], [С] и [D]- молярные концентрации (точнее активности) реагирующих веществ. ∆G⁰-изменение свободной энергии реакции при стандартных условиях, когда каждое из реагирующих веществ А, В, С и D присутствует в концентрации 1,0 М. Таким образом, ∆С реакции зависит от природы реагирующих веществ [охарактеризованной с помощью ∆G⁰ в уравнении (6)] и от их концентрации [выраженной как логарифмическая функция в уравнении (6)].

Для упрощения расчетов по изменению свободной энергии при биохимических реакциях условно принято считать, что стандартное состояние - это состояние при pH 7. Отсюда активность Н⁺, соответствующая pH 7 в уравнениях (6) и (9), равна 1. Активность воды в этих уравнениях также принята равной 1. В данной книге будет фигурировать понятие изменения стандартной свободной энергии при pH 7, обозначаемое как ∆G⁰'. В качестве единицы энергии будет использоваться килокалория

(ккал).

Можно легко вывести соотношение между стандартной свободной энергией и константой равновесия реакции. В состоянии равновесия ∆G = 0. Уравнение (6) тогда приобретает следующий вид:

(7)

и тогда

(8)

Константа равновесия при стандартных условиях, Кeq, определяется следующим образом:

(9)

Вставляя уравнение (9) в уравнение (8), получаем

∆G⁰’ = -R T In K_eq, (10)

∆G0'= -2,303 RT Ig K_eq. (11)

Преобразуя последнее уравнение, получаем

К_еq'= 10^{-∆G0/(2,303RT)} (12)

Подставив вместо R и T их значения - соответственно 1,98 • 10^-3 ккал-моль^-1 х град^-1 и Т= 298 К (25°С), получим

К_еq' = 10^{-∆G0 /1,36}, (13)

где ∆G⁰' выражено в ккал/моль. Таким образом, стандартная свободная энергия и константа равновесия реакции связаны между собой простым выражением. Например, константа равновесия 10 соответствует изменению стандартной свободной энергии —1,36 ккал/моль при 25°С (табл. 11.1).

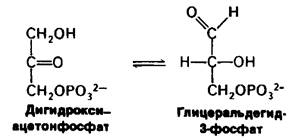
В качестве примера вычислим ∆G0 и ∆G для изомеризации дигидроксиацетонфосфата в глицеральдегид-3-фосфат. Эта реакция идет при гликолизе (гл. 12). В состоянии равновесия отношение концентрации глицеральдегид-3-фосфата к концентрации дигидроксиацетонфосфата при 25°С (298 К) и pH 7 составляет 0,0475. Изменение стандартной свободной энергии для этой реакции рассчитывается из уравнения (11):

∆G0'= -2,303RTIgKeq = - 2,303 • 1,98 • 10-3 • 298 • Ig 0,0475 = +1,8 ккал/моль.

Теперь вычислим ∆G для этой реакции, когда начальная концентрация дигидроксиацетонфосфата равна 2 • 10^-4М и начальная концентрация глицеральдегид-3- фосфата-3 • 10^-6 М. Подставляя эти величины в уравнение (6), получаем

Таблица 11.1. Связь между ∆G0' и К'_eq (при 25 С)

Отрицательное значение для ∆G указывает, что изомеризация дигидроксиацетонфосфата в глицеральдегид-3-фосфат может протекать спонтанно, когда эти соединения присутствуют в указанных выше концентрациях. Отметим, что ∆G для этой реакции имеет отрицательное значение, хотя ∆G⁰ положительно. Важно подчеркнуть, что соотношение величин ∆G и ∆G⁰ для реакции (∆Gбольше, меньше или равно ∆G⁰) зависит от концентрации реагирующих веществ. Критерием спонтанности реакции служит значение ∆G, а не ∆G⁰.

11.3. Термодинамически невыгодная реакция может быть индуцирована термодинамически выгодной реакцией

Важное значение в термодинамике имеет тот факт, что общее изменение свободной энергии для ряда реакций равно сумме изменений свободной энергии на отдельных этапах.Рассмотрим реакции

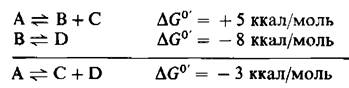
При стандартных условиях А не может спонтанно превращаться в В и С, поскольку ∆G имеет положительное значение. Однако превращение В в D при стандартных условиях термодинамически возможно. Поскольку изменения свободной энергии аддитивны, ∆G⁰ для превращения А в С и D составляет-3 ккал/моль. Следовательно, при стандартных условиях это превращение может протекать спонтанно. Таким образом, термодинамически невыгодная реакция может быть индуцирована термодинамически выгодной реакцией.Эти реакции сопрягаются при посредстве В, их общего промежуточного продукта. Мы встретимся со многими случаями сопряжения энергии в процессах обмена веществ.