Структура и функционирование белков. Применение методов биоинформатики - Джон Ригден 2014

Динамика белков: от структуры к функционированию
Молекулярно-динамические расчеты
Приложения

Молекулярно-динамические расчеты стали стандартной методикой при изучении белков и повседневно применяются при решении широкого круга задач. Конформационная динамика белков, однако, остается трудной задачей для МД расчетов, поскольку функционально значимые конформационные переходы часто совершаются за времена от микросекунд до секунд, что выходит за рамки общедоступных вычислительных алгоритмов и мощностей.

9.1.2.1. Рецепторы ядерного транспорта

Несмотря на потребность в вычислительных ресурсах, МД расчеты были успешно использованы при изучении функционирования белков. В качестве иллюстрации мы несколько глубже обсудим недавнюю работу (Zachariae and Grubmüller 2006), в которой был обнаружен поразительно быстрый конформационный переход экспортина СAS (Cselp в дрожжах) между открытым и закрытым состоянием. Белок CAS/Cselp - это состоящий из 960 аминокислот рецептор ядерного транспорта, который связывает в ядрах импортин-а и белок RanGTP. Гетеротримерный комплекс (Рис. 9.1) может проходить через ядерные поры и диссоциирует с помощью каталитического гидролиза ГТФ в цитоплазме, представляя, таким образом, важную часть нуклеоцитоплазматического траспортного цикла в клетках.

Рис. 9.1. (Цветную версию рисунка см. на вклейке.) Гетеротримерный комплекс Cselp (показан голубым), RanGTP (показан желтым) и импортина-а (показан красным). Cselp принимает сверхспиральную конформацию и связывает RanGTP и импортин-а. Комплекс может проникать сквозь ядерные поры и диссоциирует с помощью каталитического гидролиза ГТФ в цитоплазме

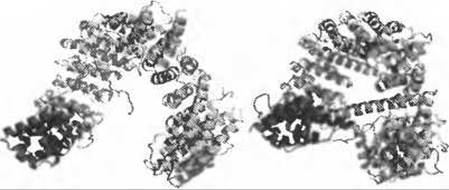
Рис. 9.2. (Цветную версию рисунка см. на вклейке.) Нуклеоплазматическая (слева) и цитоплазматическая (справа) формы Cselp. В нуклеоплазматической форме Cselp связан с RanGTP и импортином-а (оба не показаны). После диссоциации в цитоплазме Cselp претерпевает серьезные конформационные изменения и образует кольцевую конформацию, которая закрывает сайт связывания RanGTP и препятствует обратному образованию комплекса. Структуры окрашены по спектру от голубого (N-конец) до красного (С-конец)

Для функционирования системы импортин-а/CAS необходимо, чтобы после диссоциации комплекса в цитоплазме белок CAS/Cselp претерпевал сильное конформационное изменение, которое препятствовало бы обратному образованию комплекса. Рентгеновская структура белка Cselp показывает, что его загруженная конформация обладает сверхспиральной структурой, охватывая связанный RanGTP (Рис. 9.2 слева), в то время как цитоплазматическая форма этого белка имеет конформацию замкнутого кольца, что приводит к закрытию сайта связывания RanGTP (Рис. 9.2 справа). Чтобы понять механизм этого конформационного переключения, авторы провели МД расчет белка Cselp, стартовав с его загруженной конформации. Они обнаружили, что, в основном благодаря электростатическим взаимодействиям, структура белка внезапно сворачивается, и относительно быстро, в течение 10 нс, принимает конформацию, близкую к экспериментально наблюдаемой цитоплазматической форме. Расчеты МД для мутантных форм белка с различными значениями электростатического потенциала на поверхности не выявили в них значительных конформационных изменений. Напротив, эти формы сохранили открытую конформацию, что находится в хорошем согласии с экспериментальными наблюдениями (Cook et al. 2005). Этот пример показывает, что функционально значимые конформационные изменения, которые происходят на малых временных масштабах могут быть изучены с помощью МД. Однако в этом конкретном случае расчет стартовал не из равновесной конформации, поскольку импортин-а и RanGTP были удалены, и поэтому, вероятно, не было необходимости в преодолении значительного энергетического барьера для достижения закрытой конформации. Когда же расчет начинается с минимума свободной энергии, как это обычно бывает, достижимые времена расчета часто оказываются слишком малы для преодоления высоких энергетических барьеров и, следовательно, наблюдения функционально значимых конформационных переходов. Это называется проблемой сэмплирования и представляет собой общую проблему всех МД расчетов.

9.1.2.2. Лизоцим

МД моделирование лизоцима из бактериофага Т4 (T4L), фермента, в шесть раз меньшего, чем Cselp, наглядно иллюстрирует проблему сэмплирования для относительно длинных МД траекторий. Лизоцим T4L всесторонне изучался с помощью рентгеновской кристаллографии (Faber and Matthews 1990; Kuroki et al. 1993) и, будучи закристаллизован в различных конформациях, представляет собой один из редких случаев, когда информация о функционально важных состояниях может быть получена с атомарным разрешением напрямую из экспериментальных данных (Zhang et al. 1995; de Groot et al. 1998). Доменное строение этого фермента ярко выражено (Matthews and Remington 1974) и на основании различий между кристаллографическими структурами различных мутантных форм T4L было предположено, что шарнирный характер движения T4L (Рис. 9.3) является внутренне присущей чертой этой молекулы (Dixon et al. 1992).

Более того, предсказывается, что доменные флуктуации являются необходимыми для функционирования фермента, позволяя в случае открытой конформации субстрату входить в активный центр, а продуктам покидать его, в то время как каталитические превращения протекают при закрытой конформации.

Богатство экспериментальных данных предоставляет также возможность оценить надежность вычислительных методов и эффективность сэмплирования. Было выполнено два МД расчета с использованием в качестве стартовых закрытой (расчет 1) и открытой конформации (расчет 2). Для оценки эффективности сэмплирования был проведен анализ главных компонент (principal components analysis, РСА, см. Раздел 9.2 ниже) ансамбля экспериментально определенных структур, и этот ансамбль, а также две МД траектории были спроецированы на два первых собственных вектора.

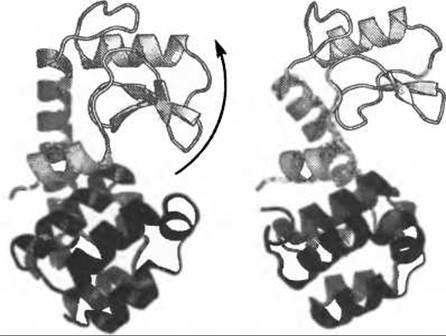
Рис. 9.3. Шарнирное движение лизоцима из бактериофага Т4. Доменные флуктуации (домены показаны разным цветом) необходимы для функционирования фермента, позволяя в случае открытой конформации субстрату входить в активный центр, а продуктам покидать его

Первый собственный вектор соответствует шарнирному движению, в то время как второй собственный вектор соответствует скручиванию доменов T4L. Проекции показаны на Рис. 9.4. Ансамбль рентгеновских структур представлен точками, каждая из которых соответствует одной конформации. Движение вдоль первого собственного вектора (ось абсцисс) описывает коллективное движение от закрытого к открытому состоянию. Легко заметить, что ни одна из МД траекторий, показанных линиями, сама по себе не охватывает все конформационное пространство, содержащее в себе ансамбль рентгеновских структур, хотя времена расчета (184 нс для расчета 1 и 117 нс для расчета 2) на порядок больше ранее обсуждавшегося времени МД расчета белка Cselp. Из плотности фазового пространства можно предположить, что существует энергетический барьер между закрытым и открытым состояниями, и ни один из расчетов не позволяет увидеть полного перехода из закрытого состояния в открытое или наоборот.

9.1.2.3. Аквапорины

Аквапорины являются лучшим примером того, какой вклад внесли МД расчеты в понимание функционирования белка с динамической и энергетической точки зрения. Аквапорины способствуют эффективному и селективному проникновению воды через биологические мембраны. Родственные им акваглицеропорины пропускают, кроме того, и небольшие нейтральные молекулы растворителей вроде глицерина. Доступные структуры высокого разрешения дали бесценную возможность взглянуть на молекулярные механизмы, действующие в аквапоринах (Fu et al. 2000; Murata et al. 2000; de Groot et al. 2001; Sui et al. 2001). Однако такие структуры несут в основном статическую информацию, и поэтому мы не можем напрямую наблюдать аквапорины “за работой”. К тому же, до сих пор нет экспериментального метода, который давал бы достаточное пространственное и временное разрешение, чтобы отслеживать проникновение через аквапорины на молекулярном уровне. Таким образом, расчеты МД дополняют экспериментальные результаты, показывая движение биомолекулярной системы с атомарным разрешением. Поскольку известно, что проникновение происходит в наносекундном диапазоне, то можно ожидать, что спонтанное проникновение будет иметь место в процессе многонаносекундных расчетов, позволяя прямое наблюдение динамики при функционировании. По этой причине такие расчеты были названы “расчетами реального времени” (de Groot and Grubmüller 2001).

Рис. 9.4. Анализ главных компонент для лизоцима из бактериофага Т4. Ансамбль рентгеновских структур показан точками, МД траектории линиями. Движение вдоль первого собственного вектора (ось абсцисс) соответствует шарнирному движению. Ни расчет 1, стартовавший из закрытой конформации, ни расчет 2, стартовавший из открытой, не демонстрируют полного перехода по причине энергетического барьера, который разделяет конформационные состояния

В самом деле, случаи спонтанного проникновения наблюдались в МД расчетах аквапорина-1 и акваглицеропорина GlpF. Эти расчеты показали, что эффективность в проникновении молекулы воды объясняется комплементарностью водородных связей внутри канала, сравнимой с таковой в объеме воды, что обуславливает низкий энергетический барьер этого события (de Groot and Grubmüller 2001; Tajkhorshid et al. 2002). Расчеты прояснили также, что селективность этих каналов объясняется двухступенчатым фильтром. Первая ступень фильтра локализована в центральной части канала в консервативной аспарагин-пролин-аланиновой (NPA) области; вторая ступень расположена на внеклеточной поверхности канала в ароматическо-аргининовой (ar/R) области сужения (Рис. 9.5) Поскольку проникновение воды происходит в наносекундном масштабе, то коэффициенты проникновения могут быть вычислены непосредственно из МД расчетов и сопоставлены с экспериментальным значением. Количественное согласие, полученное при таком сопоставлении, свидетельствует о достоверности расчетов.

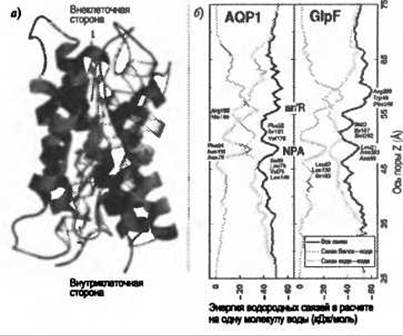
Рис. 9.5. (Цветную версию рисунка см. на вклейке.) а) Молекулы воды сильно упорядочены в канале аквапорина-1, причем их дипольные моменты направлены от центральной NPA-области (de Groot and Gmbmüller 2001). Водные диполи (показаны желтыми стрелками) поворачиваются приблизительно на 180 градусов, проходя по каналу AQP1. Красным и синим показаны локальные электростатические потенциалы, отрицательный и положительный, соответственно, б) Энергия водородных связей в расчете на молекулу воды (показана черными линиями) в AQP1 (слева) и GIpF (справа). Водородные связи белок-вода (показаны зеленым) компенсируют потерю водородных связей вода-вода (показано голубым). Главными центрами взаимодействия белок-вода являются ar/R-область и NPA-область

Долгое время в изучении аквапоринов оставался нерешенным вопрос о механизме, по которому протоны выводятся из водной поры. МД расчеты, посвященные проникновению воды, выявили отчетливую картину ориентации водных диполей в канале с центром симметрии в NPA-области (de Groot and Grubmüller 2001). Обнаружилось, что в процессе динамики молекулы воды переворачиваются на 180 градусов на своем пути по каналу (Рис. 9.5а). В ряде расчетов, посвященных выяснению механизма выведения протона, было обнаружено, что такая ориентация молекул воды вызвана электрическим полем в канале с центром симметрии в NPA-области (de Groot et al. 2003; Chakrabarti et al. 2004; Ilan et al. 2004). Таким образом, основу для выведения протона создают электростатические эффекты. Об источнике этого электростатического барьера продолжаются споры, причем были предложены как прямые электростатические эффекты, обусловленные дипольными моментами спиралей (de Groot et al. 2003; Chakrabarti et al. 2004), так и специфические эффекты десольватации (Burykin and Warshel 2003). Последние результаты позволяют предположить, что и те, и другие эффекты вносят примерно одинаковый вклад (Chen et al. 2006).

Также МД расчеты позволили прояснить механизм селективности ак- вапоринов и акваглицеропоринов к нейтральным растворителям. Было обнаружено, что аквапорины проницаемы только для небольших полярных молекул, подобных воде, за редким исключением в виде иона аммония, в то время как акваглицеропорины проницаемы также для неполярных молекул, подобных СО₂, и более крупных молекул, подобных глицерину, но не для мочевины (Hub and de Groot 2008). Для аквапоринов обнаружилось обратное соотношение между проникающей способностью растворенного вещества и его гидрофобностью - молекулы этих веществ, конкурирующие с проникающими молекулами воды за образование водородных связей с каналом, обуславливают барьер проникновения. Таким образом, в основе селективности аквапоринов и акваглицеропоринов лежит отбор по размеру и гидрофобности.