Структура и функционирование белков. Применение методов биоинформатики - Джон Ригден 2014

Динамика белков: от структуры к функционированию
Анализ главных компонент

Анализ главных компонент (Principal component analysis, РСА) является хорошо разработанной методикой для получения низкоразмерных описаний высокоразмерных данных. Его приложения включают сжатие данных, обработку изображений, визулизацию данных, научный анализ данных, распознавание образов и предсказание временных рядов (Duda et al. 2001). В контексте биомолекулярных расчетов РСА стал важным инструментом в извлечении и классификации значимой информации о крупных конформационных изменениях в ансамблях белковых структур, полученных экспериментально или теоретически (Garda 1992; Go^- et al. 1983; Amadei et al. 1993). Кроме РСА в настоящее время используется и ряд других сходных методов, среди которых стоит упомянуть анализ нормальных мод (NMA) (Brooks and Karplus 1983; Go et al. 1983; Levitt et al. 1983), квазигармонический анализ (Karplus and Kushick 1981; Levy et al. 1984a, b; Teeter and Case 1990) и сингулярное разложение (Romo et al. 1995; Bahar et al. 1997).

Анализ главных компонент основан на наблюдении, что подавляющая часть пространственных флуктуаций в белках происходит вдоль небольшого числа осей, связанный с коллективными степенями свободы. Это было впервые осознано при анализе нормальных колебаний небольших белков (Brooks and Karplus 1983; Go^- et al. 1983; Levitt et al. 1983). При таком анализе (см. раздел 9.4.1) поверхность потенциальной энергии полагается гармонической и коллективные переменные определяются диагонализацией гессиана¹ в локальном минимуме энергии. Квазигармонический анализ, анализ главных компонент и сингулярное разложение молекулярно-динамических траекторий, которые не предполагают гармоничности колебаний, показали, что и в самом деле среди колебаний потенциальной энергии в процессе динамики преобладает ограниченное число коллективных координат, причем основные моды зачастую оказываются сильно ангармоничными. Эти методы позволили выявить те коллективные степени свободы, которые наилучшим образом аппроксимируют все наблюдаемые колебания.

Наиболее сильно изменяющиеся переменные образуют набор обобщенных внутренних координат, которые можно использовать для эффективного описания динамики белка. Часто использование 5-10% от общего числа степеней свободы дает удивительно точное приближение. В отличие от внутренних координат в виде торсионных углов, эти коллективные внутренние координаты не известны заранее, а должны быть определены с использованием либо экспериментальных структур, либо ансамбля модельных структур. Как только эти коллективные степени свободы найдены, эта информация может быть использована для анализа расчетов, а также для создания улучшенных протоколов динамики с целью улучшения конформационного сэмплирования (Grubmüller 1995; Zhang et al. 2003; Не et al. 2003; Amadei et al. 1996).

¹ Матрица вторых производных потенциальной энергии d²V/dx_idx_j. Прим. автора.

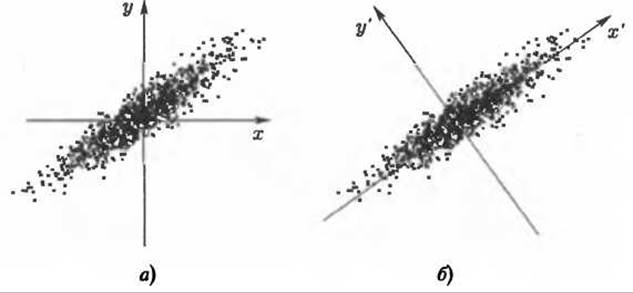
Рис. 9.7. Иллюстрация метода главных компонент (РСА) для двумерного случая. Для определения положения точки из ансамбля нужны две координаты (х, у) (б), в то время как для приблизительного определения положения достаточно одной координаты х' (а)

В сущности, метод главных компонент - это многоразмерный метод наименьших квадратов в пространстве конфигураций. Ансамбль структур молекулы, имеющей N атомов, может быть представлен в 3N-мерном пространстве конфигураций, как облако точек, где каждая конфигурация представлена одной точкой. Для такого облака всегда может быть определена ось, вдоль которой наблюдается максимальный разброс точек. Как показано для двумерного случая (Рис. 9.7), если такая линия хорошо соответствует данным, то положение каждой точки может быть аппроксимировано одной лишь проекцией на эту ось, что дает разумную аппроксимацию даже при отбрасывании проекций на остальные направления, перпендикулярные этой оси. Если выбрать эту ось в качестве координатной, то положение точки может быть описано одной координатой. В общем 314-мерном случае процедура выполняется аналогично.

Зная ось, которая в первом приближении описывает данные наилучшим образом, можно выбрать ортогональные направления для второго приближения, третьего приближения и так далее (главные компоненты). Все вместе эти направления охватывают 314-мерное пространство. Математически эти направления задаются собственными векторами μ_i ковариационной матрицы флуктуаций атомов

где угловые скобки <•> означают усреднение по ансамблю. Собственные числа λ_і соответствуют средним квадратам пространственных флуктуаций вдоль соответствующих собственных векторов и, таким образом, показывают вклад каждого главного компонента в общую флуктуацию (Рис. 9.8)

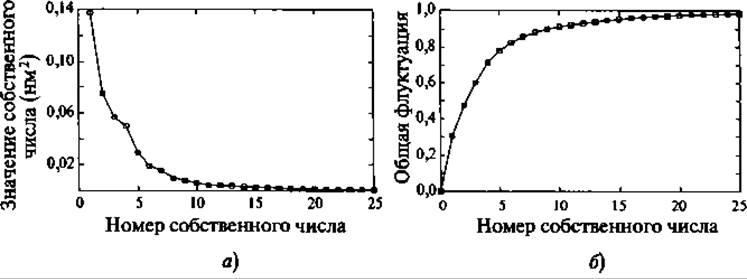
Рис. 9.8. Типичный спектр собственных значений в методе главных компонент (МД ансамбль структур основной цепи гуанилина). Первые пять собственных векторов (панель а) покрывают 80% всех наблюдаемых флуктуаций (панель б)

Применение таких процедур многоразмерной подгонки к конфигурациям белков из МД расчетов показало на нескольких примерах, что обычно первые 10-20 главных компонент ответственны за 90% флуктуаций белка (Kitao et al. 1991; Garda 1992; Amadei et al. 1993). Эти главные компоненты соответствуют коллективным координатам, содержащим вклад от каждого атома белка. В ряде случаев было показано, что эти главные моды являются частью функциональной динамики изучаемых белков (Amadei et al. 1993; Van Aalten et al. 1995a, b; de Groot et al. 1998). По этой причине подпространство, отвечающее за большую часть флуктуаций, было названо коллективным подпространством (essential subspace) (Amadei et al. 1993).

Тот факт, что небольшая часть от общего числа степеней свободы (основное подпространство) доминирует в молекулярной динамике белков, имеет место из-за большого количества внутренних ограничений, которые определяются взаимодействием атомов в биомолекуле. Такими взаимодействиями являются как сильные ковалентные связи, так и слабые невалентные взаимодействия, в то время как ограничения задаются плотной упаковкой атомов в нативной структуре.

В целом, динамика белков при физиологических температурах была описана как диффузия среди множества минимумов (Kitao et al. 1998; Amadei et al. 1999; Kitao and Go^- 1999). В динамике на малых временах преобладают колебания возле локального минимума, соответствующие собственным векторам с низкими собственными значениями. В больших колебаниях на больших временах преобладает ангармоническая диффузия между многочисленными потенциальными ямами. Такие медленные динамические переходы в методе главных компонент обычно представлены модами с большими амплитудами. В отличие от анализа нормальных мод, применение метода главных компонент к МД траектории не основывается на предположении о гармоническом потенциале. В самом деле, метод главных компонент может быть использован для изучения степени ангармоничности в молекулярной динамике моделируемой системы. Было показано, что для белков при физиологической температуре среди главных мод коллективных флуктуаций, зачастую функционально значимых, преобладают ангармонические флуктуации (Amadei et al. 1993; Hayward et al. 1995).