Структура и функционирование белков. Применение методов биоинформатики - Джон Ригден 2014

Распознавание фолда
“Протягивание”
Эвристические правила выравнивания

Поскольку проблема протягивания формально не решаема (является NP-сложной), было разработано множество эвристических правил, предназначенных для высокочувствительного отбора возможных выравниваний в процессе поиска псевдооптимального решения за разумное вычислительное время. Один из подходов состоит в использовании ограничений для положения и размера разрывов. Суть состоит в том, что разрывы допускаются только в наиболее вероятных областях структуры шаблона, например, между консервативными элементами вторичной структуры (Madej et al. 1995). Еще один подход известен как “замороженное приближение” (рис. 2.3, слева) (Westhead et al. 1995). Как уже было отмечено выше, основная проблема при расчете оценки выравнивания определенного остатка относительно положения в структуре шаблона состоит в том, что выравнивание всех остальных остатков, то есть, окружение исследуемого остатка, должно быть известно. А поскольку оно неизвестно, при использовании фиксированного приближения за него принято принимать окружение последовательности шаблона. Это изящное и простое решение будет, несомненно, удачной аппроксимацией в тех случаях, когда исследуемая последовательность близка к последовательности шаблона. Однако этот способ неприемлем, если между последовательностями имеются существенные различия, то есть, именно в том случае, который нас интересует.

Более утонченный вариант фиксированного приближения разработан Сколником и Кихара (Skolnick and Kihara 2000) и носит название “размороженное приближение” (рис. 2.3, справа). В этом случае источником окружения остатка служит не структура шаблона, а первичное пробное выравнивание исследуемой последовательности относительно структуры шаблона, полученное с использованием классических методов выравнивания на основе профилей. Это значит, что по крайней мере окружение исследуемого остатка основано на верной последовательности. Тем не менее, достоверность получаемых в итоге значений энергии существенно зависит от качества первичного выравнивания, которое, как мы помним, являлось проблемой изначально. Чтобы уменьшить зависимость метода от первичного выравнивания, процесс многократно повторяют, каждый раз выравнивая последовательность с учетом вклада, который вносят оценки протягивания, полученные в ходе предшествующих повторений.

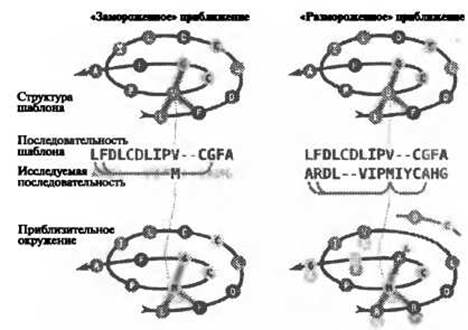
Рис. 2.3. (Цветную версию рисунка см. на вклейке.) Схематичное представление протягивания. Слева: замороженное приближение: здесь остаток М исследуемой последовательности предварительно выровнен относительно остатка V структуры шаблона. Затем производится оценка эмпирического потенциала для остатка М в окружении остатков G, L и F, взятых непосредственно из нативной структуры шаблона. Справа: размороженное приближение. Сначала выполняется пробное выравнивание. Можно использовать, например, методики выравнивания профилей. Теперь за окружение остатка М теперь принимается окружение из пробного выравнивания. Тенями показаны остатки исходного шаблона

Довольно сложный подход, разработанный Джонсом с сотр. (Jones et al. 1992) и названный “двойным динамическим программированием”, используется в программе THREADER. Эффективность подхода была продемонстрирована в ранних испытаниях CASR Полное описание методики лежит за пределами настоящей главы, однако общая идея состоит в выравнивании одиночного положения в исследуемой последовательности относительно одиночного положения в структуре шаблона. Затем для выравнивания оставшейся части последовательности используется традиционный алгоритм выравнивания, который позволяет оптимизировать потенциал относительно этого фиксированного положения. Оптимальное выравнивание, обнаруженное таким образом, позже добавляют в оценочную матрицу. Процесс повторяют для каждой возможной пары остатков последовательности и структуры (или по крайней мере для большого количества значимых пар), при этом информация об оптимальном выравнивании всякий раз заносится во вторичную оценочную матрицу. Наконец, вторичная оценочная матрица используется для создания окончательного выравнивания, в котором учитывается максимально возможное количество накопленных оптимальных выравниваний. Именно из-за такого двухуровневого выравнивания метод называется двойным динамическим программированием. Первоначально метод предназначался для разделения проблемы протягивания на множество небольших задач, сочетание решений которых давало однозначный ответ. Эта идея позже неоднократно использовалась во многих методах, описываемых ниже.

Алгоритм сэмплирования Гиббса применялся для решения проблемы протягивания Бриантом (Bryant 1996). В случае применения этой методики на первом этапе выполняется случайное выравнивание. На каждом шаге алгоритма случайным образом выбирается элемент вторичной структуры ядра С, для него создаются все возможные альтернативные выравнивания, для каждого нового выравнивания рассчитывается оценка S, а затем осуществляется выбор нового выравнивания с вероятностью, пропорциональной exp(-S/kT), где k - постоянная Больцмана, а Т — воображаемая “температура” системы. Каждая новая итерация предполагает использование нового случайным образом выбранного элемента ядра в качестве мишени для выравнивания. Используется протокол имитации отжига, с помощью которого “температура” системы со временем медленно снижается. Использование высокой температуры на начальном этапе приводит к тому, что выравнивания с низкими оценками учитываются так же часто, как и выравнивания, оцениваемые высоко. Это приемлемо для начального этапа моделирования, поскольку вероятность получить полное выравнивание высокого качества случайным образом очень мала. Тем не менее, по мере того, как температура падает, постепенно снижается вероятность учета выравниваний с низкими оценками, и система “оседает” на выравнивание с глобально низкой энергией. Имитация отжига широко используется для решения проблем оптимизации в биоинформатике и других областях. Метод не гарантирует нахождение выравнивания, соответствующего глобальном оптимуму, однако характеризуется быстротой и высокой производительностью.

При использовании алгоритма протягивания “разделяй и властвуй” (Xu et al. 1998) осуществляется многократное разделение структуры на подструктуры, для которых решается проблема выравнивания, и полученные для них решения объединяются для нахождения глобального оптимального выравнивания. Схожим образом в алгоритме поиска ветвей и границ (Lathrop and Smith 1996) пространство поиска протягивания многократно делится на подпространства меньшего размера, среди которых осуществляется отбор наиболее удачного подпространства, которое затем снова делится. На завершающем этапе наиболее удачное из отобранных подпространств содержит лишь одно выравнивание, которое и является глобальным оптимумом. Нахождение глобального оптимума требует очень больших временных затрат, в связи с чем была разработана версия программы, условно называемая “Всегда готов!”, (Lathrop 1999), с помощью которой быстро удается получить довольно точное приближение. Чем дольше процесс выполнения программы, тем точнее получаемые результаты. В конечном счете, программа возвращает выравнивание, соответствующее глобальному оптимуму.

Еще один подход, тесно связанный с описанным, - протягивание белка с помощью линейного программирования (Xu et al. 2003). Линейное программирование - общий метод, который используется для решения сложных задач при наличии ряда ограничений. В случае протягивания к числу таких ограничений часто относится представление о том, что выравнивание определенной области исследуемой последовательности относительно структуры подразумевает аналогичное выравнивание последующих (предыдущих) частей последовательности относительно соответствующих последующих (предыдущих) частей структуры. Ограничения такого типа, будучи скорее логическими переменными, чем непрерывными, могут все вместе рассматриваться как задача целочисленного программирования. Такие задачи часто решают, представляя их менее строго - как непрерывные задачи линейного программирования, после чего следует применение модели ветвей и границ.

Приведенный обзор некоторых методов протягивания демонстрирует, насколько широкий набор инструментов из области физики, математики и компьютерных наук использовался для решения этой сложной задачи в последние 15-20 лет. Тем не менее, до сих пор не существует единого метода, который обладал бы выраженным превосходством над другими методами в этой области. Несмотря на наличие высокопроизводительных и точных методов выравнивания последовательности относительно структуры, основанных на использовании энергетической функции, именно энергетическая функция представляется тем “слабым звеном”, которое является основной причиной низкой производительности.