БИОЛОГИЯ Том 3 - руководство по общей биологии - 2004

ПРИЛОЖЕНИЯ

Приложение 2. Биологические методы

П.2.1. Научный метод

Наука — это совокупность фактических знаний о материальном мире и законах его развития, полученных с помощью научных методов.

«Наука практически полностью есть результат удовлетворения

любознательности мыслящего человека.»

А. Уайтхед

Чтобы удовлетворить собственную любознательность, ученые должны постоянно ставить вопросы, касающиеся устройства окружающего нас мира. Правильно сформулированный вопрос — залог успеха науки.

«Сформулировать проблему часто бывает важнее, чем найти ее решение,

которое нередко зависит от умения пользоваться математическим

аппаратом и опыта экспериментатора. Способность ставить новые вопросы,

видеть новые возможности, рассматривать старые проблемы под новым углом зрения

требует творческого воображения и приводит к подлинным успехам в науке».

А. Эйнштейн

Научная работа может явиться продолжением уже сделанных наблюдений или может быть следствием некоего внутреннего «индуктивного» процесса, происходящего в умах ученых. Истинно научные утверждения, как подчеркивает современный гносеолог Карл Поппер, должны быть доступны для проверки и воспроизведения другими исследователями. Поэтому очень важно, чтобы все научные исследования были полностью и ясно описаны, как это показано в разд. П.2.2. Если при повторных исследованиях в одинаковых условиях получены одинаковые результаты, то их можно признать достоверными. Знания, которые невозможно проверить таким образом, относятся к разряду «метафизических», а не научных.

Факты основываются на прямых или косвенных наблюдениях, выполненных с помощью органов чувств или приборов, таких как свето- или радиотелескопы, световые и электронные микроскопы, осциллографы, действующих как усилители наших чувств. Все факты, относящиеся к конкретной проблеме, называются данными. Наблюдения могут быть качественными (т. е. описывать цвет, форму, вкус, внешний вид и т. д.) или количественными. Количественные наблюдения являются более точными. Они включают измерение величины или количества, наглядным выражением которых могут служить качественные признаки.

В результате наблюдений получают так называемый «сырой материал», на основе которого формулируется гипотеза (рис. П.2.1). Гипотеза — это основанное на наблюдениях предположение, с помощью которого можно дать убедительное объяснение наблюдаемых явлений. Эйнштейн подчеркивал, что гипотеза выполняет две функции:

1) она должна объяснять все наблюдаемые явления, относящиеся к данной проблеме;

2) она должна вести к предсказанию новых знаний. Новые наблюдения (факты, данные), подтверждающие гипотезу, будут способствовать ее упрочению, тогда как наблюдения, противоречащие гипотезе, должны привести к ее изменению или даже к отказу от нее.

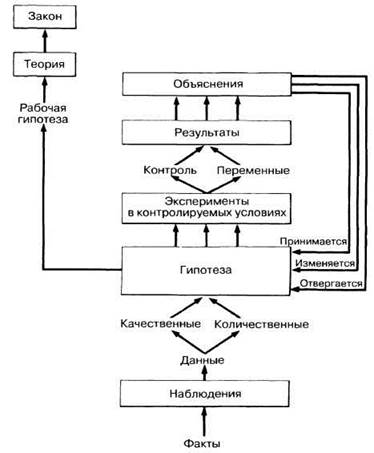
Рис. П.2.1. Схематичное изображение научного метода.

Для того чтобы оценить обоснованность гипотезы, необходимо запланировать серию экспериментов с целью получения новых результатов, подтверждающих или противоречащих гипотезе. В большинстве гипотез обсуждается ряд факторов, которые могли бы повлиять на результаты научных наблюдений; эти факторы называются переменными. Гипотезы можно объективно проверить в серии экспериментов, в ходе которых поочередно исключается по одной из предполагаемых переменных, влияющих на результаты научных наблюдений. О такой серии экспериментов говорят, что она проводится в контролируемых условиях. Иными словами, в каждом конкретном случае проверяется влияние только одной переменной.

Наиболее удачная гипотеза становится рабочей гипотезой, и если она способна устоять при попытках ее опровержения и по-прежнему удачно предсказывает ранее необъясненные факты и взаимосвязи, то она может стать теорией.

Общее направление научного исследования состоит в достижении более высоких уровней предсказуемости (вероятности). Если теорию не способны изменить никакие факты, а встречающиеся от нее отклонения регулярны и предсказуемы, то ее можно возвести в ранг закона.

По мере увеличения совокупности знаний и совершенствования методов исследования гипотезы и даже прочно укоренившиеся теории могут оспариваться, видоизменяться и даже отвергаться. Научные знания по своей природе динамичны и рождаются в процессе полемики, а достоверность научных методов постоянно подвергается сомнению.

П.2.2. Работа в лаборатории и протоколирование эксперимента

Прежде чем начать любое экспериментальное исследование, необходимо ясно представить себе цель эксперимента. Цель может состоять в проверке гипотезы, такой, например, как: «Для прорастания семян необходимо наличие воды, кислорода и оптимальной температуры», или в проведении более широкого исследования: например: «Как влияет свет на поведение мокрицы?». В обоих случаях план эксперимента необходимо составить таким образом, чтобы он был выполним, а полученные данные были достоверны и могли успешно использоваться для получения тех или иных выводов.

Описание эксперимента необходимо проводить в строгой логической последовательности.

1. Название. В названии должна быть ясно сформулирована суть исследуемой проблемы. Например: «Эксперимент по изучению влияния pH на активность фермента». В названии необходимо развернуто сформулировать замысел, который конкретизируется при изложении гипотезы или цели.

2. Гипотеза или цель. Это изложение проблемы или постановка вопроса. Оно может включать перечисление исследуемых переменных и предсказание возможных результатов исследования. Например: «Изучить влияние растворов с pH от 2 до 10 на скорость переваривания белка альбумина ферментом пепсином и определить оптимум pH для этой реакции».

3. Методика или процедура. Это перечень действий, производимых во время выполнения эксперимента. Он должен быть кратким, точным и приводиться в том же порядке, в котором установлены приборы и производятся действия во время эксперимента. Метод нужно описывать в прошедшем времени и не от первого лица. Пользуясь этим описанием, другие исследователи должны быть в состоянии повторить эксперимент.

4. Результаты и наблюдения. Они могут быть качественными или количественными и должны быть представлены как можно яснее в соответствующей форме или формах. Например, в виде словесного описания, таблиц с данными, графиков, гистограмм, карт, диаграмм распределения и т. д. Если при повторных измерениях одной переменной получено несколько числовых значений, то необходимо подсчитать и записать среднее значение этой переменной.

5. Обсуждение. Оно должно быть кратким и проводиться в форме ответов на возможные сформулированные в гипотезе вопросы или же в форме подтверждения цели. Обсуждение не должно быть словесным повторением результатов. В нем нужно попытаться связать теоретические знания об исследуемых переменных с полученными результатами.

Заключение можно делать в том случае, если было получено убедительное подтверждение исходной идеи. Например, в качестве заключения на приведенную в п. 2 тему исследования можно привести следующее утверждение: «Между величиной pH и активностью фермента существует определенная зависимость, оптимальное значение pH равно л». Обсуждение результатов этого же эксперимента должно включать такие теоретические вопросы, как природа реакции и возможные химические и физические аспекты влияния pH на трехмерную структуру молекул фермента.

П.2.3. Представление данных

После проведения качественных и количественных исследований получают определенные результаты в виде описательных и численных данных. Чтобы получить максимальное количество информации, необходимо тщательно спланировать исследование, а полученные данные всесторонне обработать и тщательно проанализировать.

П.2.3.1. Составление таблиц

Таблицы относятся к наиболее простому способу представления данных. Они состоят из колонок со значениями двух или более связанных переменных. С помощью этого метода трудно получить прямое и ясное указание на связь между переменными, но он часто является первым этапом регистрации информации и служит основой для выбора последующей формы графического представления данных.

П.2.3.2. Графическое представление данных

График — это двумерное изображение зависимости между двумя или более переменными. График самой простой формы строится на двух осях. По вертикальной оси (оси у) откладываются значения, называемые ординатами, которые показывают величину зависимой переменной, т. е. функции. Это — «неизвестное количество», иными словами переменная, значения которой не выбираются экспериментатором. Горизонтальная ось л: несет значения, называемые абсциссами, которые показывают величину независимой переменной. Это — «известное количество», т. е. переменная, значения которой выбираются экспериментатором.

График строится следующим образом:

1. Масштаб и интервалы на каждой оси должны выбираться в соответствии с величинами переменных, значения которых откладываются на графике таким образом, чтобы максимально использовать место на бумаге.

2. Каждая ось должна начинаться с 0, но если все значения одной переменной расположены близко друг к другу, например между 6,12 и 6,68 лежит десять точек, то, чтобы разместить эти точки, потребуется крупный масштаб. В этом случае ось также начинают с 0, но сразу после нуля на оси делается отметка о разрыве в виде знака -//—.

3. На каждой оси необходимо указать название и размерность переменной, например «Температура, °С». Ось должна быть разделена на равные интервалы, например от 0 до 60 на 12 интервалов по 5 единиц в каждом.

4. Точки, отмеченные на графике, называются координатами. Они представляют соответствующие значения двух переменных, например когда х = а, а у = b.

5. Точки, нанесенные на основе фактических данных, необходимо отмечать кружком, крестиком или точкой в кружке, а не просто точкой.

6. Отмеченными на графике точками регистрируются фактические наблюдения. Точки могут соединяться серией прямых отрезков, начерченных по линейке, плавной кривой или в некоторых случаях кривой регрессии (линия наибольшего соответствия) (разд. П.2.4.3). Такие графики называются линейными. Точки лучше соединять прямыми отрезками или плавной кривой, а не кривой регрессии.

7. Графику необходимо дать развернутое название, например: «График, показывающий связь между...».

8. Фактические данные представлены только точками, нанесенными на график, оценки же других значений можно получить, измерив координаты любой точки, лежащей на линии. Этот метод называется интерполяцией. Сходным образом, продолжив линию, можно определить координаты крайних точек графика. Этот метод известен как экстраполяция. В обоих случаях необходимо подчеркнуть, что полученные значения являются приблизительными.

По графикам, на оси х которых откладывается время, можно подсчитать крутизну кривой или градиент любой точки. Эта величина соответствует скорости изменения исследуемой переменной. Например, на графике, показанном на рис. П.2.2, скорость роста подсчитывают путем проведения касательной к кривой в требуемой точке и построения треугольника, в котором эта касательная является гипотенузой (рис. П.2.3). Затем значение отрезка у делят на значение отрезка х и получают скорость изменения в единицах, отложенных по осям графика.

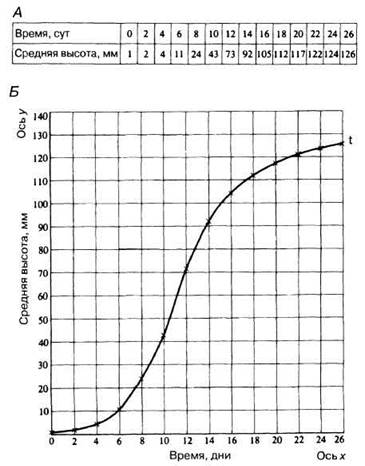
Рис. П.2.2. А. Два ряда данных: средняя высота проростков овса и продолжительность их роста. Б. График зависимости между средней высотой проростков овса и продолжительностью роста.

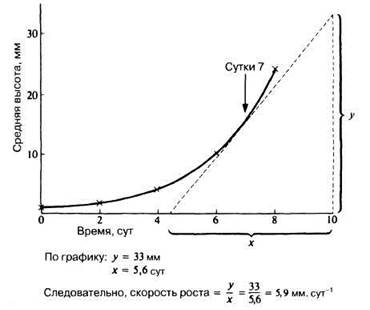
Рис. П.2.3. Метод определения скорости изменения в данной точке, например на седьмой день.

П.2.3.3. Распределение частот

Существует множество отношений между переменными, при которых каждое значение зависимой переменной, соответствующее значению независимой переменной, представляет собой число событий, приходящихся на данное значение независимой переменной, т. е. ее частоту. Такие отношения можно описать функцией распределения частот, или просто распределением, например распределением дождевых червей по длине тела в популяции.

Если независимая переменная может принимать любые значения в пределах данного ряда, то распределение частот можно представить в виде обычного графика, как это описано выше. Такие графики называются кривыми распределения и в зависимости от рода данных могут иметь одну из форм, описанных ниже. Если данные представляют собой численность организмов в пределах определенного интервала, как показано на рис. П.2.4, А, то распределение называется непрерывным, а все пространство под кривой составляет общую частоту событий.

1. Кривая нормального распределения. В этом случае распределение частот симметрично относительно центрального значения, а рассматриваемые переменные относятся к физическим параметрам, таким как рост или масса биологического объекта. Этот тип распределения показан на рис. П.2.4.

2. Положительный уклон. Кривая распределения в этом случае несимметрична. Наибольшие частоты независимой переменной приходятся на ее более низкие значения, а по направлению к более высоким значениям кривая начинает «хвостить» (рис. П.2.5, А). В качестве примера такого распределения можно привести распределение числа детей, приходящихся на одну семью, размеров кладки у птиц, плотности фитопланктона с увеличением глубины.

3. Отрицательный уклон. В этом случае наибольшие частоты независимой переменной приходятся на ее более высокие значения, а по направлению к более низким значениям кривая начинает «хвостать» (рис. П.2.5, Б). Эта форма распределения встречается реже, чем предыдущая; она характерна для распределения некоторых форм смещения. Например, распределение оптимальных температур ферментативных реакций и выработка тироидстимулирующих гормонов в ответ на действие тироксина.

4. Бимодальное распределение. В этом случае наблюдаются два максимума (или два пика), что обычно указывает на присутствие двух популяций, для каждой из которых характерно неполное нормальное распределение.

5. Совокупное распределение частот. Данные, представленные на рис. П.2.4, можно также представить, как на рис. П.2.6. Здесь показано совокупное число организмов, находящихся ниже определенного произвольно выбранного класса границ. Если эти данные изобразить графически, то получится кривая совокупного распределения частот.

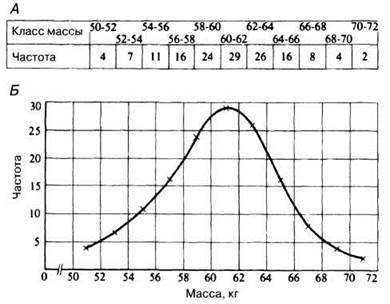
Рис. П.2.4. А. Представленная в виде таблицы численность 18-летних мужчин в каждом классе массы по 2 кг. Б. Графическое изображение данных из табл. А дает кривую нормального распределения.

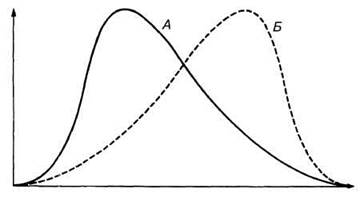
Рис. П.2.5. А. Распределение с положительным уклоном. Б. Распределение с отрицательным уклоном.

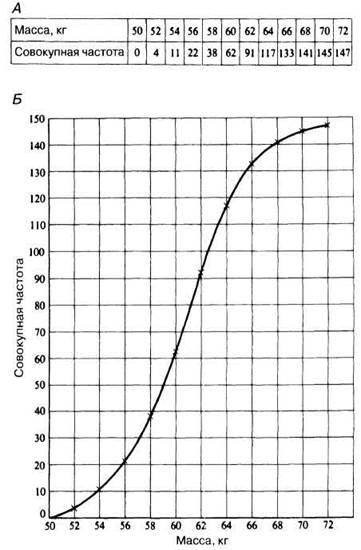
Рис. П.2.6. Таблица (А) и график (Б), построенные на основе рис. П.2.4, А, представляющие совокупную частоту распределения массы среди 18-летних мужчин.

Если независимая переменная принимает дискретные значения, например целые числа 3 и 5 (как число лепестковудвудольных), или ею представлены физические признаки, такие, например, как группы крови, которые характеризуются дискретными значениями, то распределение не будет непрерывным. В этом случае нельзя начертить непрерывную кривую, поэтому используются другие, описанные ниже формы графического изображения данных.

1. График в виде вертикальных столбцов. Он показывает частоту, с которой определенные признаки встречаются внутри популяции, например частота групп крови у человека (см. рис. П.2.7, А).

2. Гистограмма. Она строится на непрерывных значениях независимой переменной, сгруппированных в классы равной ширины. Когда классы равной ширины выбраны, например 0—5, 5—10, 10—15 и т. д., границы интервалов обычно проходят по числам меньшим, чем указанные целые значения, т. е. 0—4,99; 5—9,99; 10—14,99 и т. д. В форме гистограммы удобно представлять данные, характеризующие небольшие выборки. Внешне гистограммы похожи на диаграммы в виде вертикальных столбцов (рис. П.2.7, Б).

3. Диаграмма в виде горизонтальных столбцов. Это видоизмененная форма гистограммы. Она обычно используется для того, чтобы показать отношения между непрерывной зависимой переменной, например содержанием энергии, и нечисловой независимой переменной, например различными видами пищи (рис. П.2.7, В). Видоизмененная форма горизонтальной диаграммы используется для представления экологических данных; она называется диаграммой присутствия-отсутствия (см. рис. 11.22).

4. Лоскутная диаграмма (кайт-диаграмма). Это особый тип горизонтальной диаграммы, который дает предельно ясное наглядное изображение изменения частот неисчисляемых переменных, непрерывно распределенных в пределах определенной площади. Кайт-диаграмма строится путем нанесения частот каждой переменной в виде параллельных отрезков, перпендикулярных оси х (см. рис. П.2.8, А).

После того как все частоты нанесены вдоль оси х, соседние концы отрезков соединяются прямыми линиями как при построении линейного графика (см. рис. П.2.8, Б). Заключенную внутрь фигуры площадь обычно заштриховывают, чтобы получить более наглядное изображение. О применении кайт-диаграмм распределения рассказано в разд. 11.4.3.

Каждый из перечисленных выше способов представления данных используется при решении различных биологических задач. Эти способы изложены в различных главах книги. Каждый метод имеет свои достоинства. При выборе того или иного метода следует руководствоваться тем, как можно наиболее точно и рационально продемонстрировать связи и характер отношений между переменными.

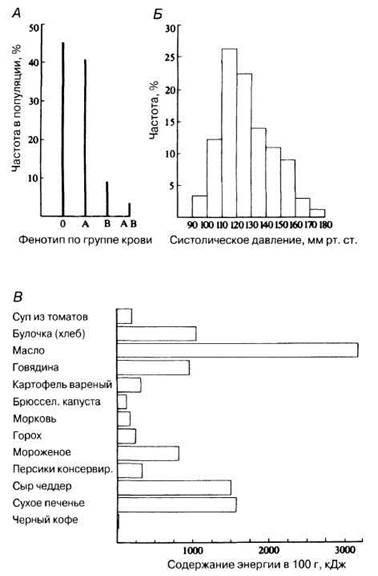
Рис. П.2.7. Способы представления данных. А. График с вертикальным расположением столбцов, показывающий фенотипы по группам крови в популяции. Б. Гистограмма, показывающая частоту различного систолического кровяного давления у женщин в возрасте от 30 до 39 лет. В. Диаграмма с горизонтальным расположением столбцов, показывающая содержание энергии в пище (при трехразовом питании).

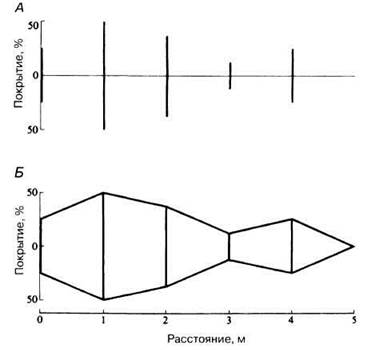
Рис. П.2.8. Способы построения лоскутной, или кайт-диаграммы (от англ. kite — бумажный змей).

П.2.4. Основные статистические методы в биологии

После того как данные записаны в виде ряда характеризующих переменные значений, например таких как рост или частота сокращений сердца, полезно определить их среднее значение и разброс значений. Оценки среднего значения называются «характеристиками расположения относительно центра». Они включают среднее, медиану и моду. Оценки разброса величин называются «мерой рассеяния», они включают дисперсию и стандартное отклонение.

П.2.4.1. Характеристики расположения относительно центра

Среднее (среднее арифметическое)

Это «средняя величина» группы значений, которую получают путем сложения всех значений и деления суммы на число сложенных значений. Например, среднее (х) для значений х₁, х₂, х₃, х₄... х_n подсчитывается следующим образом:

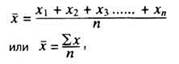
где Σ — сумма или общее количество, х — отдельное значение и n — число отдельных значений.

Если одно и то же значение х встречается более чем один раз, среднее можно подсчитать, используя выражение

где Σf — сумма частоты встречаемости х, или проще — n.

Медиана

Она представляет собой среднее, или центральное, значение группы переменных. Например, если пять значений х расположены в следующей последовательности: х₁, х₂, х₃, х₄ и х₅, то значение медианы будет равно х₃, так как равное число значений расположено до и после х₃. Если число значений четное, например от x₁ до х₆, то медиана будет равняться среднему из двух срединных значений

Мода

Это — значение переменной, встречающееся наиболее часто. Например, если число детей в десяти семьях соответственно равно 1, 1, 1, 2, 2, 2, 2, 2, 3, 4, то мода равна 2.

Каждое из трех значений, описанных выше, имеет свои преимущества и недостатки и применяется при решении определенных задач. Проиллюстрировать применение среднего или моды можно на примере с различным числом детей в семьях. Среднее число детей в семье составляет 2,4, но так как ребенок — величина дискретная, естественно описывать число детей в целых числах, т. е. с помощью моды, которая равна 2.

В случае нормального распределения значения среднего, медианы и моды совпадают (рис. П.2.9, А). В случае того или иного уклона частоты распределения их значений — не совпадают (рис. П.2.9, Б).

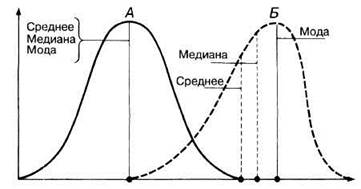
Рис. П.2.9. Положение среднего, медианы и моды при нормальном распределении (А) и при распределении с уклоном (Б)

П.2.4.2. Оценки дисперсии

Для того чтобы оценить, в какой мерю значения признака отклоняются от среднего, вычисляют среднее и дисперсию. Для нормального распределения это проиллюстрировано двумя кривыми на рис. П.2.10. При статистическом анализе данных очень информативной является оценка среднего квадратичного, или стандартного, отклонения; по этим показателям можно предсказать и распределение значений вокруг среднего, и ответить на вопрос, достоверна ли разница между двумя группами данных.

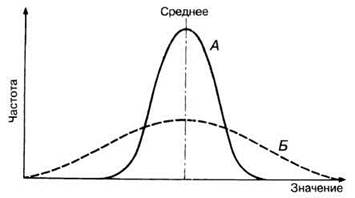
Рис. П.2.10. Две кривые нормального распределения, демонстрирующие распределение двух совокупностей данных (возможно, характеризующих популяцию) с одинаковой общей частотой (т. е. площади под кривыми равны). Кривая А построена по ограниченному ряду значений, сгруппированных вокруг среднего. Кривая Б построена по широкому ряду значений, не сгруппированных вокруг среднего.

Стандартное отклонение

Стандартное отклонение (s) совокупности данных служит мерой отличия этих данных от среднего арифметического. Для его подсчета используют выражение

где Σ — сумма, f — частота, х — отдельные значения и — среднее. Например, в выборке из десяти раковин блюдечка (Patella vulgaris), отобранных на скалистом берегу, эти раковины имеют следующие максимальные значения диаметров в миллиметрах: 36, 34,41,39, 37,43, 36, 37, 41, 39. Чтобы определить среднее максимальное значение диаметра и стандартное отклонение, необходимо вычислить f, fx² и х², как это показано в следующей таблице:

Следовательно, = 38,3 и ²= 1466,9.

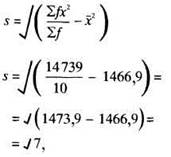
следовательно, s = 2,65.

В этой популяции имеющих общее происхождение блюдечек среднее максимальное значение диаметра раковины равно 38,3 мм, а стандартное отклонение равно 2,7 мм (округлили до одной десятой). Если эти значения применить к более крупной популяции блюдечек общего происхождения, то на основе статистики можно предположить, что приблизительно 68% популяции будет иметь диаметр раковины 38,3 мм плюс-минус одно стандартное отклонение (2,7 мм), т. е. размеры раковин будут лежать в интервале от 35,6 до 41,0 мм; приблизительно 95% популяции будут иметь диаметр раковины 38,3 мм плюс-минус два стандартных отклонения (5,4 мм), т. е. диаметры будут лежать в интервале 32,9—43,7 мм, а практически 100% будут лежать в интервале плюс-минус три стандартных отклонения от 38,3 мм.

По величине стандартного отклонения можно судить о разбросе данных. Если стандартное отклонение мало, то, следовательно, разброс (отклонение от среднего) невелик и популяция в значительной степени однородна, как это показано на рис. П.2.10, А. С увеличением стандартного отклонения увеличивается степень изменчивости внутри популяции, как показано на рис. П.2.10, Б.

Дисперсия

Дисперсия — это квадрат стандартного отклонения. Дисперсия совокупности значений подсчитывается по следующей формуле:

где f — число значений в совокупности.

Дисперсию обычно подсчитывают в экологических исследованиях, включающих изучение питания, размножения и поведения, поскольку она служит показателем распределения организмов внутри популяции. Распределение может быть:

а) случайным;

б) групповым;

в) регулярным.

Для того чтобы определить тип распределения организмов внутри популяции, исследуемую площадь делят на квадраты равного размера (см. разд. 11.2) и подсчитывают число организмов этой популяции в каждом квадрате. Исходя из этих данных, подсчитывают значение дисперсии по следующей формуле:

где f — число квадратов, содержащих х организмов. Используя выражение

Распределение популяции = Дисперсия/Среднее,

можно выделить три типа распределения (рис. П.2.11).

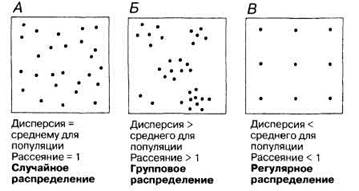
Рис. П.2.11. Типы распределения.

П.2.4.3. Связь между переменными

Данные всегда необходимо представлять таким образом, чтобы можно было выявить связи между двумя или более их совокупностями. Проще всего это сделать с помощью графика или диаграммы, показывающих связь между переменными. Но это целесообразно только в том случае, если одна из переменных (независимая переменная) находится под контролем экспериментатора, как, например, в случае, приведенном на рис. П.2.2.

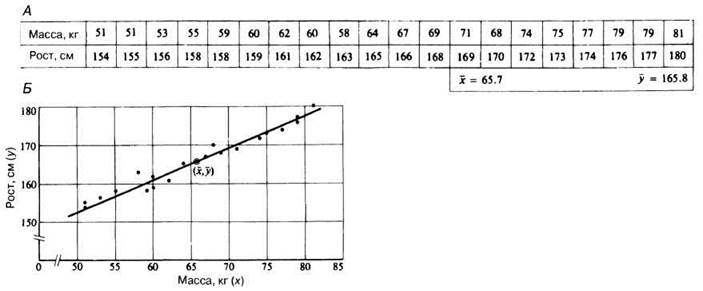
Рис. П.2.12. Данные о массе и росте у двадцати 16-летних студентов мужского пола представлены в виде таблицы (А) и диаграммы рассеяния (Б). Построена кривая регрессии.

В других случаях, когда обе переменные являются независимыми, составляют таблицу, в которой значение одной помещают под соответствующим значением другой, как, например, в случае данных о росте и массе 20 студентов шестого курса, приведенных на рис. П.2.12, А. на основе этих данных вычерчивают график (рис. П.2.12, Б), который называется диаграммой рассеяния. По внешнему виду графика видно, что эти две переменные связаны между собой некоторым образом, но эту связь, представленную прямой линией, невозможно описать более точно до тех пор, пока все данные не будут представлены на графике в виде точек.

Эта линия называется «линией наибольшего соответствия», или линией регрессии. Мера приближения точек к линии указывает на степень корреляции между двумя переменными. Линия наибольшего соответствия должна проходить через точку, соответствующую среднему значению массы и роста а число точек над и под линией должно быть приблизительно одинаковым. По этой линии можно подсчитать рост, соответствующий определенной массе.

Корреляция

Описанную выше связь между двумя переменными х и у можно обозначить термином корреляция. Между х и у могут существовать различные степени корреляции, как это показано на диаграммах рассеяния на рис. П.2.13.

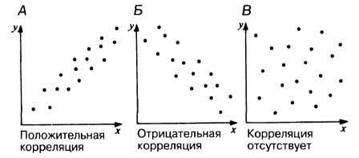
Рис. П.2.13. Типы корреляции; А — положительная корреляция; Б — отрицательная корреляция; В — корреляция отсутствует.

С помощью диаграммы рассеяния нельзя точно продемонстрировать статистическую достоверность корреляции, так как этот способ субъективен. Достоверность корреляции можно представить с помощью статистического критерия, называемого коэффициентом корреляции. Его величина может изменяться от —1 до +1; —1 означает полностью отрицательную корреляцию, например отрицательную корреляцию между давлением кислорода в атмосфере и скоростью открывания дыхалец у насекомых; 0 означает отсутствие корреляции, например отсутствие корреляции между размерами плодов томатов и числом семян в них; +1 означает полностью положительную корреляцию, например положительную корреляцию между возрастом и длиной тела у саранчи.