Биологические мембраны - А. Н. Огурцов 2012

Электрогенез биомембран
Неравновесная термодинамика биомембран
Обобщённые силы и обобщённые потоки

Многие биологические процессы реализуются только в неравновесном состоянии, поскольку протекают под действием неравновесных сил, образующих, в свою очередь, потоки различного рода. Целенаправленное создание и поддержание определённых неравновесных условий протекания биотехнологических процессов зачастую является ключевым фактором повышения эффективности частных биотехнологий.

Биологическая система, находящаяся в равновесном состоянии, "мертва", для нее не существует времени и истории. В это состояние она перешла из неравновесного состояния, когда система была ещё "живой" и обладала "силами", которые производили различные изменения, которые и привели систему в состояние равновесия, т. е. к "смерти". Этого можно избежать, если искусственно поддерживать биосистему в состоянии далеком от термодинамического равновесия.

В неравновесной термодинамике термины "сила" или "обобщённые силы" приписываются всем воздействиям или изменениям, включая обычные механические силы. Так, например, в длительном неравновесном состоянии систему может поддерживать постоянный приток и отток вещества и энергии. Поэтому в данном контексте свойства необратимости процесса и неравновесности представляют собой две стороны одного и того же явления физического мира.

В неравновесной системе могут возникать силы, например, за счёт протекания химических реакций, температурных и концентрационных градиентов, являющихся разностью соответствующих величин в различных участках данной системы.

Силы образуют течения, или потоки, которые, в конце концов, истощают силы, их породившие. Все градиенты постепенно исчезают, и система достигает окончательного состояния равновесия.

Например, температурный градиент между двумя точками предмета является источником движущей силы и порождает поток теплоты - перенос из горячей в холодную часть тела некоторого количества теплоты через единичную площадь в единицу времени. Этот поток теплоты увеличивает температуру холодного участка за счёт горячего и постепенно приводит систему к состоянию теплового равновесия.

Наличие сил и потоков в неравновесной системе означает, что эта система неоднородна, и что в ней происходят химические процессы.

Стандартным приемом при описании неоднородных систем является разбиение системы на бесконечно малые объёмы, в каждом из которых систему можно считать однородной, при этом можно строго определить локальные переменные и интегральные свойства всей системы получать, суммируя по всему объёму системы. Так, для у-го компонента системы вводится р_у - парциальная масса единицы объёма (парциальная плотность), при этом плотность определяется как

Для системы из n молей используем молярные величины

Тогда можно ввести локальные величины - энтропия единицы объёма (локальная энтропия); - внутренняя энергия единицы объёма (локальная энергия).

Объём больше не является независимой переменной, поскольку

Локальная энтропия является функцией локальной энергии и парциальных плотностей и эта функциональная зависимость описывается локальным уравнением Гиббса

которое является частным случаем уравнения Гиббса

где N_y - масса данного компонента в одном моле вещества системы.

Общая энтропия системы может быть получена интегрированием локальной энтропии по всему объёму системы

Свойства необратимости и неравновесности состояния выражаются термодинамически через "производство" энтропии (изменение энтропии со временем), и наша задача - связать изменение локальной энтропии во времени с силами (градиентами, сродством) и потоками, которые обеспечивают неравновесность системы.

Производная по времени локальной энтропии

как функции нескольких переменных

где р'_у≠ р_у и р_у - все независимые переменные, сумма которых

отличие от закрытых систем может не быть постоянной.

Из локального уравнения Гиббса

получаем соотношение

Следовательно,

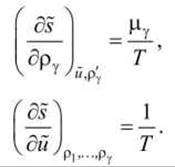
Далее, чтобы определить потоки воспользуемся гидродинамическими соотношениями, основанными на законе сохранения массы.

Закон сохранения массы требует, чтобы изменение во времени массы вещества в некоторой области системы (если взять единичный объём, то, фактически, это будет изменение плотности вещества) обуславливалось только потоками вещества через границу этой области. При этом неоднородность системы, как и прежде, учитывается введением локальных переменных, использованием плотности, вместо массы, устремлением объёма V, рассматриваемой области к нулю, то есть переходом от интегральных параметров к локальным (в данной точке системы).

В этом случае закон сохранения массы связывает производную парциальной плотности данного компонента у по времени в данной точке пространства со скалярным потоком векторного поля - диффузионным потоком вещества наружу через поверхность, окружающую данную точку.

Для обеспечения локальности мы устремляем объём области под поверхностью к нулю, и получаем выражение

Таким образом, это соотношение является математической записью закона сохранения массы - в данной точке плотность вещества может уменьшиться только за счёт положительного потока вещества наружу через поверхность, замыкающую бесконечно малый объём вокруг данной точки.

Кроме потока вещества изменение плотности вещества в данной точке может происходить за счёт химических реакций, из которых образуется данный компонент (которые являются источниками данного компонента).

В этом случае необходимо добавить соответствующее слагаемое в правую часть уравнения

где v_r - скорость; v_ry - стехиометрический коэффициент у-го компонента в r -й реакции.

Совершенно аналогично, закон сохранения энергии требует, чтобы локальное изменение энергии в данной точке (в отсутствии процессов конвекции, механической работы или любых других внешних сил) происходило только за счёт потока энергии через такую же поверхность, окружающую данную точку, поэтому запишем

Если теплота - единственная форма внутренней энергии, то локальное изменение внутренней энергии связано с потоком теплоты

Подставим теперь в уравнение

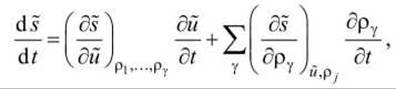
значения из выражений

получим

где

В действительности нужно учесть ещё источник энтропии за счёт необратимых процессов, введя дополнительное слагаемое с

Первое слагаемое в правой части - потоковый член - дивергенция векторного поля потока энтропии который обусловлен двумя процессами:

1) тепловым потоком

2) диффузионным потоком химических веществ

Второе слагаемое а описывает интенсивность локального производства энтропии (источник энтропии), вызванного различными необратимыми процессами под действием обобщённых сил Xi, которые являются причиной появления соответствующих обобщённых потоков

Векторные обозначения здесь опущены, поскольку обобщённые потоки и обобщённые силы могут быть и скалярными величинами. В нашем случае в химической реакции роль обобщённой силы играет сродство, а роль обобщённого потока выполняет скорость химической реакции

Общее изменение энтропии системы

можно представить в виде двух слагаемых.

Энтропия системы может изменяться как за счёт (1) потока энтропии через границу Ω системы

так и за счёт (2) производства энтропии внутри системы

Если мы изолируем систему от внешних энтропийных потоков, то, согласно второму началу термодинамики, энтропия изолированной системы может только увеличиваться, следовательно

или

откуда следует условие

Таким образом, сумма всех значений величин J_iX_i не должна быть отрицательной, хотя при этом отдельные значения J_iX_i могут быть отрицательными.

Заметим, что в литературе используют также так называемую диссипативную функцию Ф (или функцию диссипации), которая равна интенсивности производства энтропии, умноженной на температуру

Обобщённые потоки зависят от обобщённых сил (поскольку ими вызываются), и, наоборот, скорость химической реакции зависит от сродства, поток тепловой энергии - от разности температур. Запишем в общем виде эту функциональную зависимость как

В состоянии равновесия обобщённые силы обращаются в нуль и не вызывают никаких потоков.

Вблизи равновесия величина обобщённых сил мала и, соответственно, величина потоков тоже мала. Поэтому, разложив потоки в ряд Тейлора

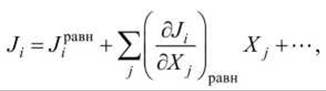
мы можем ограничиться только линейными членами (по определению J_і^равн = 0)

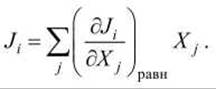
Область применимости такого линейного подхода называется термодинамикой линейных необратимых процессов.

Феноменологические коэффициенты пропорциональности между обобщёнными потоками и обобщёнными силами

рассчитываются в равновесном состоянии. В линейном приближении

Когда і = j, то коэффициенты L_ii называются прямыми (несопряжёнными) коэффициентами, они отражают тот факт, что в данный поток вызывает своя же собственная сила.

Когда і ≠ j (два индекса различны), L_ij, коэффициенты называются сопряжёнными, и в этом случае они означают, что сила j создаёт поток і.

Примером линейного процесса является закон Ома

который в дифференциальной форме имеет вид

или (поскольку

и рассматривая одномерный ток вдоль оси х)

где R - электрическое сопротивление проводника; у - удельная электрическая проводимость проводника; - напряжённость электрического поля; I - сила электрического тока; j - плотность электрического тока; φ - потенциал электрического поля; U - напряжение.

Некоторые примеры линейных необратимых процессов вида J = LX и соответствующих сопряжённых обобщённых сил и порождаемых ими обобщённых потоков приведены в таблице 6.