Биологические мембраны - А. Н. Огурцов 2012
Электрогенез биомембран
Неравновесная термодинамика биомембран
Сопряжение потоков в биомембранах
Организм, клетка - это химические машины, функционирующие в результате химических реакций и переноса вещества между клеткой и окружающей средой, а также внутри клетки. Перенос имеет определённое направление, перпендикулярное к внешней клеточной и внутриклеточным биомембранам.
Поток вещества есть вектор. В то же время скорость химической реакции - скаляр. Прямое сопряжение скалярного и векторного процессов в изотропной среде невозможно в силу принципа Кюри - Пригожина. Однако биомембраны являются принципиально анизотропными системами, построенными из молекул, лишенных плоскости и центра симметрии. Именно анизотропность мембран позволяет сопрягать скалярные и векторные процессы - процессы переноса вещества с химическими реакциями. Наличие мембран обеспечивает прерывистость биосистем. Биомембрана является той перегородкой, которая позволяет поддерживать разность параметров среды по разные стороны мембраны, обеспечивая скачок какого-либо параметра системы (например, концентрации какого-либо компонента или электрического потенциала) на мембране.
Рассмотрим сначала пример, в котором водный раствор сахарозы находится в двух отсеках А и В, разделённых мембраной М (рисунок 166).
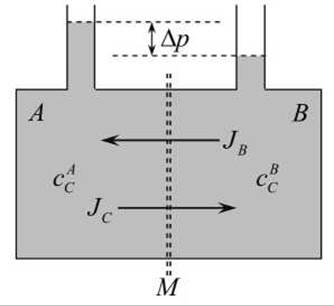
Рисунок 166 - Пассивный транспорт веществ через мембрану М
Мембрана частично проницаема для молекул сахарозы и полностью проницаема для молекул воды (растворителя). В результате через мембрану устанавливаются два потока - сахарозы JC и воды JB. Диссипативная функция для этих двух потоков
![]()
В изотермических условиях движущая сила для обоих потоков имеет вид
![]()
где ∆р - разность гидростатических давлении в двух отсеках, ∆μ - разность химических потенциалов вещества по обе стороны мембраны, ![]() - парциальный молярный объём вещества. Тогда
- парциальный молярный объём вещества. Тогда
![]()
или
![]()
Разность химических потенциалов ∆μс связана с осмотическим давлением μπ, которое компенсирует разницу в концентрациях растворов по обе стороны мембраны. Согласно закону Вант-Гофа
![]()
Для химического потенциала
![]()
при dμ0 = 0. Для рассматриваемого примера представим ∆μс через небольшое приращение химического потенциала
![]()
Где ![]() - средняя концентрация сахарозы в системе
- средняя концентрация сахарозы в системе
![]()
Следовательно,
![]()
Связь двух сопряжённых потоков, растворённого вещества и растворителя, подчиняется уравнению Гиббса-Дюгема
![]()
Следовательно,
![]()
С учётом этого диссипативная функция имеет вид
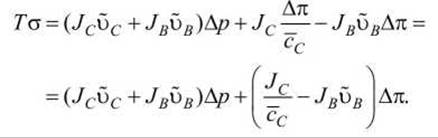
Таким образом, диссипативная функция представлена новыми обобщёнными силами (Ар и Ал) и новыми потоками
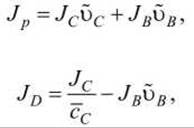
где Jp - объёмный поток; JD - диффузионный поток. Теперь
![]()
Для сопряжённых потоков Jр и JD в соответствии с уравнениями
![]()
запишем
![]()
Определим смысл феноменологических коэффициентов.
Во-первых, рассмотрим ситуацию, когда концентрация сахарозы одинакова по обе стороны мембраны сА = сB. При этом ∆π = 0. Следовательно,
![]()
Таким образом, разница в гидростатическом давлении вызывает объёмный поток Jp и добавочный диффузионный поток JD, который приводит к перераспределению сахарозы.
Это явление называется ультрафильтрация, а коэффициент LDp называется коэффициентом ультрафильтрации.
Во-вторых, рассмотрим случай, когда гидростатическое давление одинаково по обе стороны мембраны, т. е. ∆р = 0, тогда
![]()
Коэффициент Ldd называется коэффициентом проницаемости вещества через мембрану.
Добавочный объёмный поток Jp называется осмотическим потоком, а коэффициент LpD - коэффициентом осмотического потока. Используя соотношение взаимности Онзагера Lij =Lji, получим связь между потоками
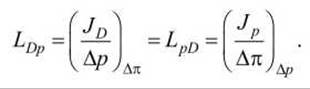
Теперь рассмотрим ситуацию, когда объёмный поток Jр = 0. Тогда
![]()
Введем новую постоянную к, которая называется коэффициентом отражения (константой Ставермана)
![]()
Коэффициент отражения к зависит от свойств мембраны. Запишем объёмный поток с учётом к
![]()
Рассмотрим две гипотетические крайние ситуации. Если к = 1, то растворённое вещество совсем не проникает через мембрану (полностью "отражается" от мембраны), тогда
![]()
Если к = 0, то мембрана полностью проницаема и
![]()
Коэффициент отражения к показывает механизм переноса вещества через мембрану. Он равен нулю в случае, если LpD = 0, а это означает, что нет сопряжения между потоками Jр и JD - перенос растворителя происходит независимо от переноса растворённого вещества. В реальных ситуациях к ≤ 1 и LpD≠ 0, что указывает на связь между потоками Jр и JD. Это существенное обстоятельство, которое часто игнорируется, когда (ошибочно) рассматривают процессы переноса воды и веществ в клетку независимо. Только применение положений линейной неравновесной термодинамики и использование соотношения взаимности Онзагера к явлениям переноса через клеточную мембрану позволяют количественно верно описывать транспорт веществ в клетку.
Следует также помнить, что биологические мембраны принципиально отличаются от искусственных небиологических полупроницаемых мембран (например, пористых резиновых перегородок, разделяющих две жидкие фазы) существованием процессов облегчённого и активного транспорта, которые можно описать, только используя методы неравновесной термодинамики.
Например, Nа+/К+-АТФаза обеспечивает одновременный перенос ионов натрия и калия через мембрану. Мы можем выделить "обменную" силу
![]()
которая описывает общий ионный обмен через мембрану. Суммарный обменный поток Jобм обозначает, что ионы К+ обмениваются на ионы Na+.
Остальные (r, rest) сопряжённые силы Хr обеспечивают химические потоки Jr. Тогда производство локальной энтропии внутри мембраны
![]()
и, соответственно, в линейном приближении
![]()
По определению в активном транспорте поток Joбм направлен против действия сил Joбм. Это возможно только тогда, когда коэффициенты L12 = L21 не равны нулю.
Действительно, согласно условию Lіі > 0 коэффициент L11 должен быть положительной величиной. Следовательно, если L12= 0, то из Jобм = L11Xобм + L12Xr следует, что Jобм и Jобм должны иметь одинаковый знак, и активный транспорт становится невозможным. Если же сопряжённый член L12Xr принимает отрицательные значения, направление потока Jобм обращается против силы Joбм.
Из уравнения σ = XoбмJoбм + XrJr видно, что активный транспорт вносит отрицательный вклад в производство энтропии, уменьшая её значение. Без сопряжения потоков и сил различного рода процессы, приводящие к понижению значения энтропии, были бы невозможны.
Рассмотрим два процесса, которые протекают в везикулах, содержащих протонный насос (Н+-АТФазу): JH - поток протонов Н+ и Jр - гидролиз АТФ, которые представим в виде:
![]()
где ХН = ∆μН+; LРН = LHР; Хр - изменение свободной энергии при расщеплении АТФ. Химическая энергия гидролиза АТФ JpXp, трансформируется в энергию транспорта протонов JHХH.
Введем коэффициент трансформации η, который при условии Ф = JHXH + JpXp > 0 равен
![]()
Если определить безразмерную величину
![]()
- степень сопряжения, для которой -1 < q < 1 (при q = 1 химическая энергия трансформируется в другой вид энергии на 100%), то можно показать, что максимальный коэффициент трансформации равен
![]()
В любой системе есть потери энергии, следовательно, величина q должна быть меньше 1.
Если увеличивается ХH, то при наличии транспорта протонов значение η уменьшается. В то время как в закрытых системах коэффициент сопряжения между обычными реакциями выражается целыми числами, в открытых системах, например, в случае окислительного фосфорилирования в биомембранах, сопряжение между процессами потребления кислорода и фосфорилирования выражается дробным числом.
Как уже говорилось выше, любая открытая система вообще (и биомембраны в частности) может находиться в стационарном, хотя и неравновесном состоянии.
Это состояние характеризуется постоянным значением энтропии. Живой организм существует в этом состоянии при условии, что при изменении одних параметров другие сохраняют постоянное значение.
В нашем примере изменение энтропии к объёму с учётом L12 = L21 будет равно
![]()
где сила Х2 обозначена через фиксированное значение Х02 = const. Дифференцируем это выражение по X1
![]()
откуда
![]()
представляют собой постоянные величины, пропорциональные X02.
Иными словами, в стационарном состоянии, близком к равновесию, изменение энтропии минимально. Это состояние подобно равновесному состоянию в закрытых системах. Как уже отмечалось, за счёт сопряжения различных потоков могут протекать процессы, характеризующиеся отрицательным изменением энтропии в других потоках.
Это явление компенсации потока с отрицательной энтропией является одним из необходимых условий обеспечения жизнедеятельности организма.