Основы биохимической инженерии Часть 1 - Бейли Дж., Оллис Д. 1989

Молекулярная генетика и системы регуляции
Рост и самовоспроизведение изолированной клетки
Клеточный цикл эукариот

Прежде всего нам следует вспомнить, что в природе не существует типичной эукариотической клетки. В то же время модель такой воображаемой клетки оказывается очень полезной при обсуждении черт, свойственных большинству эукариот; именно в этом смысле мы будем использовать понятие о типичной эукариоте в настоящем разделе.

Возможные различия между разными типами эукариотических клеток легко оценить, если, например, проанализировать увеличение клеточной массы в процессе жизненного цикла клеток мыши и амебы (рис. 6.33). В то время как масса сухих веществ клеток мыши возрастает во времени линейно или экспоненциально, скорость роста клеток амебы постепенно уменьшается и в момент деления становится практически равной нулю. Второй вариант более типичен для эукариот вообще. Обратите внимание также на шкалу времени — клеточный цикл этих эукариот длится около суток. Впрочем, некоторые эукариотические организмы, например дрожжи, в оптимальных условиях могут делиться примерно раз в час.

Для клеточного цикла эукариот характерна (по сравнению с прокариотами) высокая степень дифференциации между отдельными периодами цикла. Обычный цикл эукариотической клетки изображен на рис. 6.34. Он подразделяется на четыре периода: G₁, S, G₂ и М; относительные продолжительности этих периодов указаны на рисунке. В периоде G₁ происходит активный синтез белков и РНК, а ДНК не синтезируется. В следующем периоде 5 осуществляется репликация хромосом. Функция периода G₂ пока еще достаточно достоверно не выяснена. Вслед за этим периодом начинается деление клеток (период М). Сложный, хорошо координированный процесс деления эукариот называют митозом. В митозе два набора хромосом разделяются и распределяются по дочерним клеткам. В медленно растущих или нерастущих культурах клетки находятся в состоянии покоя, обозначаемом символом G₀.

В отличие от характерной для прокариот линейной временной зависимости синтез ферментов в эукариотах почти всегда осуществляется периодически. В определенный момент клеточного цикла наблюдается резкое повышение концентрации того или иного фермента. Имеющиеся экспериментальные данные позволяют предположить, что в основе этого явления лежит последовательный характер транскрипции ДНК.

В качестве примера, иллюстрирующего структуру клеточного цикла эукариот и асимметричное деление клеток, вкратце рассмотрим жизненный цикл размножающихся почкованием дрожжей 5. cerevisiae. Этот микроорганизм широко применяется в пивоварении, производстве пищевых продуктов и генетической инженерии. Как показано на рис. 6.35, дочерняя клетка растет на материнской в виде почки. Затем, после деления, материнская клетка быстро возвращается в начальную фазу цикла почкования, в то время как обычно сравнительно небольшая дочерняя клетка должна еще в течение какого-то времени расти; только после этого она достигает типичного для начала цикла почкования состояния («старт»).

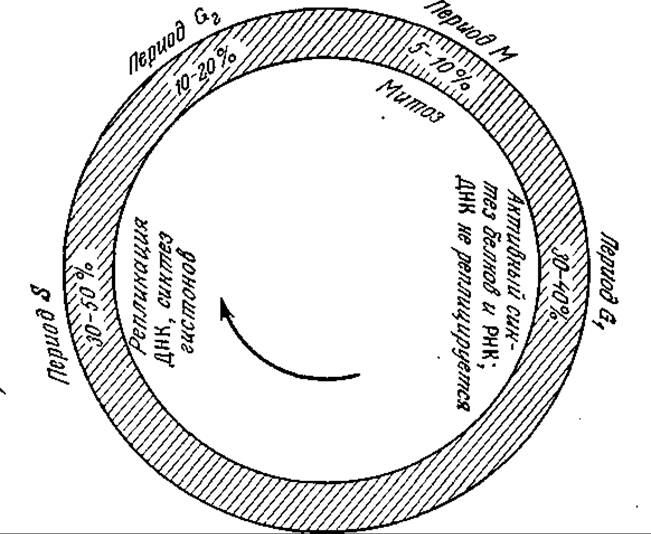
РИС. 6.34. Последовательность событий в жизненном цикле типичной эукариотической клетки.

РИС. 6.35, Клеточный цикл почкующихся дрожжей S. cerevisiae.

Начало периода 5 примерно совпадает с появлением почки. Все непочкующиеся клетки находятся в периоде G₁. Если обратиться к изображенному на рис. 6.30 распределению ДНК в индивидуальных клетках 5. cerevisiae, можно достаточно обоснованно предположить, что первый пик отвечает клеткам с одним геномом, т. е. клеткам, находящимся в периоде G₁. Второй пик отвечает клетками с двумя геномами, которые могут находиться в одном из двух периодов — G₂ или М. Математический анализ распределений подобного типа позволяет быстро определить относительные времена пребывания клеток 5. cerevisiae в периодах G₁, S и G₂+M и таким образом изучать влияние генетических изменений и среды на регуляцию клеточного цикла.

В этом разделе мы ознакомились с некоторыми особенностями клеточных циклов. В сущности, в настоящее время о них имеется чрезвычайно мало данных. Как показало изучение клеточного метаболизма (гл. 5), для эффективной утилизации питательных веществ клетке необходима тщательнейшая координация чрезвычайно сложной сети химических реакций. Биохимия этих реакций известна достаточно детально, однако мы почти ничего не знаем о том, как они осуществляются in vivo. На рис. 6.36 приведены интересные данные, свидетельствующие о наличии сложных закономерностей в распределении отдельных взаимосвязанных реакций во времени. Следовательно, химические реакции в клетке локализованы не только в пространстве (например, за счет иммобилизации фермента на поверхности мембраны), но и во времени. Все эти сложные эффекты вынуждают нас проявлять крайнюю осторожность, если перед нами стоит задача математического анализа кинетики роста живых клеток.

Этим мы заканчиваем наше введение в биологические науки. Вооруженные полученными в этой и предыдущих главах знаниями, мы должны быть готовы к изучению технологии процессов с участием живых клеток. Основное внимание в последующих главах мы уделим анализу, моделированию и проектированию биологических процессов. В гл. 7 рассмотрена кинетика клеточного роста.

РИС. 6.36. Сложный характер изменения относительного содержания свободных аминокислот в течение клеточного цикла в Chlorella pyrenoidsa. [Воспроизведено с разрешения из статьи: Hare Т. A., Schmidt R. R., Nitrogen Metabolism During Synchronous Growth of Chlorella: II. Free-, Peptide-, and Protein- Amino Acid Distribution, J. Cell Physiol., 75, 73 (1970).]

Упражнения

6.1. Частота мутаций. Мутации приводят к новым видам, мутантам. Поскольку ДНК представляет собой всего лишь полимерную молекулу, в ходе мутаций она, вероятно, претерпевает какие-либо химические и физические изменения точно так же, как и молекулы любого другого соединения.

а) Исходя из приведенных на рис. 6У1.1,а данных, вычислите энергию активации мутации Е_m и предэкспоненциальный множитель k°_m в уравнении k_m = k°_mexp (—E_m/RT). Сравните вычисленные величины с аналогичными параметрами для более простых соединений, претерпевающих химические превращения. (Эти данные вы можете взять из любого учебного пособия по органической химии.)

б) Поглощение излучения подчиняется закону Бера, согласно которому каждый компонент мишени поглощает одну и ту же часть излучения, падающего на этот компонент; следовательно, I(х) = I₀e^-ах. На рис. 6У1.1.6 изображена линейная зависимость частоты мутаций от интенсивности излучения І₀. При каких условиях все клетки могли получить одинаковую дозу радиации? Можно ли ожидать линейную зависимость частоты мутаций от дозы, если не все клетки получат одинаковую дозу радиации?

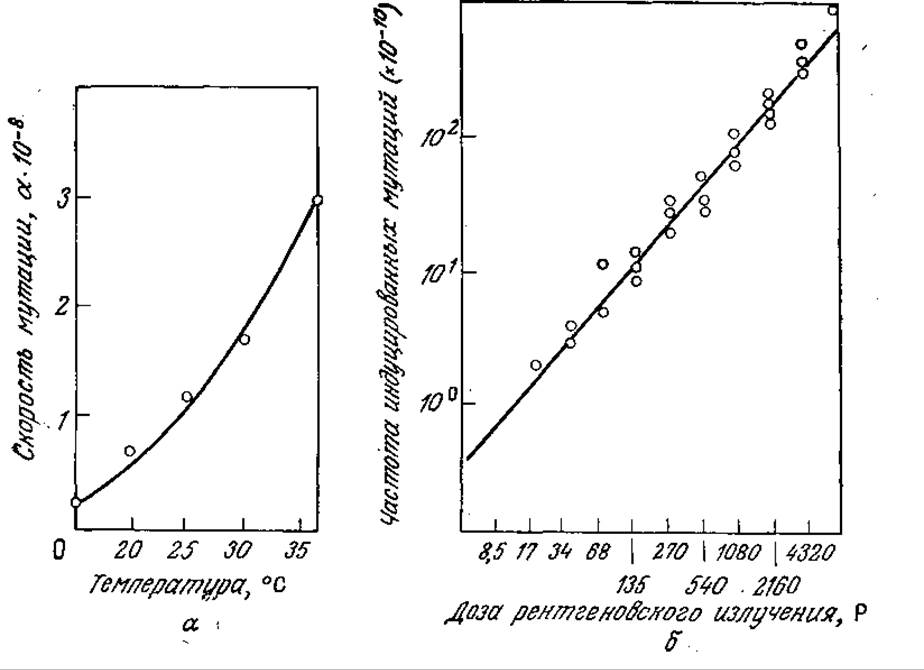
РИС. 6У1.1. Скорость мутаций Е. coli возрастает при повышении температуры и дозы ионизирующего излучения, а — влияние температуры на частоту мутаций his^-(неспособных синтезировать гистидин бактерий) в his⁺ (синтезирующие гистидин организмы); б — влияние дозы рентгеновского излучения на превращение организмов met-2^- (не синтезирующих метионин) в мутанты met-2⁺(синтезирующие метионин). (Воспроизведено из работы: Sager R., Ryon F. Cell Heredity: An Analysis of the Mechanisms of Hereditary at the Cellular Level, John Wiley and Sons, Inc., New York, 1961.)

в) Приведенные на рис. 6У1.1 данные относятся к популяциям Е. coli, мутирующим от his^-(неспособных синтезировать гистидин) к his⁺ (рис. 6У1.1,а) и от met-2-(неспособных синтезировать метионин) к met-2⁺. Если любые изменения ДНК осуществляются с такой же вероятностью, как и в указанных случаях, какова общая скорость мутации ДНК Е. coli? Обоснуйте ваш ответ. Характерно ли для этих мутаций фенотипическое проявление?

6.2. Репарация и термодинамика мутаций. Если в процессе участвует большое число организмов, то кинетику мутаций можно описать теми же параметрами, какие используются в кинетике обычных химических реакций.

а) В популяции бактерий с концентрацией клеток 3∙10⁷ мл^-1 (объем культуры 1000 л) мутация гена в ген g₂ происходит с частотой 10^-8 на деление клетки, а обратная мутация g₂ в g₁ — с частотой 10^-6 на деление клетки. Вычислите «равновесные» концентрации каждого мутанта.

б) Поскольку в клетках, способных ферментативным путем репарировать повреждения ДНК, имеется соответствующий специфический фермент, можно предположить, что в таких случаях имеет место и равновесие между нормальной и поврежденной ДНК:

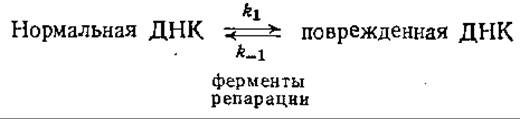
Предположим, что ДНК повреждается еще и ультрафиолетовым излучением; константа скорости этой реакции равна k¹. Покажите, что в этом случае равновесная популяция поврежденной ДНК повышается от k₁/(k₁+k_-1) до (k¹+k₁) / (k₁+k¹+k_-1).

в) Покажите, что после отключения источника ультрафиолетового излучения (при условии, что К_m репарационного фермента значительно превышает общую концентрацию ДНК) средняя концентрация поврежденной ДНК возвратится к исходному уровню со скоростью, пропорциональной разности концентраций поврежденной ДНК в отсутствие и при наличии ультрафиолетового излучения.

6.3. Упрощенная модель кинетики действия репрессора. Дж. М. Смит предложил упрощенную схему сети кинетической регуляции, изображенную на рис. 6У3.1.

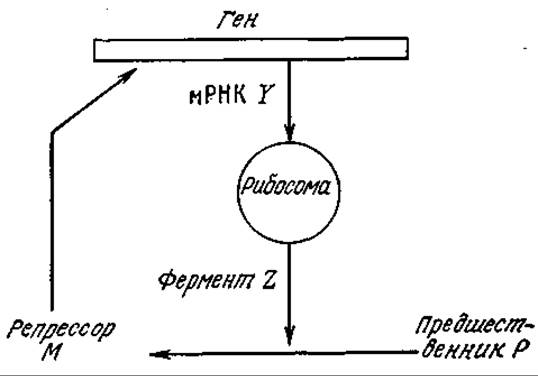
РИС. 6У3.1. Упрощенная модель механизма действия репрессора. (Воспроизведено из работы: Smith J. М., Mathematical Ideas in Biology, fig. 30, Cambridge University Press, London, 1971.)

а) Приняв, что концентрации P и гена стационарны, разработайте кинетическую модель, описывающую (после решения соответствующих уравнений) зависимость концентраций РНК, М и Z от времени. Считайте, что скорость потери РНК пропорциональна ее концентрации. Постарайтесь, насколько эта только возможно, приблизиться к полному решению для переходного состояния.

б) Основываясь на материале этой и предыдущих глав, укажите, должна ли в данном случае приниматься во внимание диффузия, и отметьте недостатки модели.

6.4. Мутация и генетический код. В мутантных белках обнаружены указанные ниже замены аминокислот. Объясните, какие кодоны подверглись.

6.5. Организация внутриклеточных превращений; многоферментные системы. Многие реакции в клетке протекают путем превращения S₁ в S₃ через промежуточное соединение S₂, причем по сравнению с S₁ и S₃ равновесная концентрация S₂ мала:

Если S3 участвует в следующей катализируемой ферментом реакции, то обратимостью второй реакции можно пренебречь.

а) Приняв, что для каждого фермента s_i ≪ K_i и что S₁ и S₂, E₁и Е₂ распределены в объеме равномерно, покажите, что скорость реакции в стационарном состоянии определяется следующим выражением:

б) Покажите, что если E₁закреплен на одной стороне проницаемой пластины, а Е₂ — на другой, то скорость реакции в стационарном состоянии будет подчиняться уравнению

Покажите также, что эта величина меньше, чем s_{2 e}qullD/L, где L — расстояние между поверхностями пластины, a s_2,equll— концентрация S₂, находящегося в равновесии с S₁ при концентрации последнего s₁.

в) Обычно скорость поглощения кислорода равна 10^-8 моль/(с∙см³). Приняв, что скорости каждой из стадий внутреннего метаболизма примерноодинаковы, вычислите максимальное расстояние между E₁ и Е₂, при котором была бы возможной указанная скорость поглощения кислорода, если величина s₂,_equll составляет от 10^-4 до 10^-12 моль/см³. [Weisz Р. В., Enzymatic Reaction Sequences and Cytological Dimensions, Nature, 195, 772 (1962).]

6.6. Организация внутриклеточных превращений; синтез и утилизация

АТР. В интактной клетке имеются локализованные центры (органоиды), призванные снабжать всю клетку определенными соединениями. В этой связи представляется интересным рассмотреть сперматозоиды быка, в которых АТР синтезируется только в промежуточном отделе сперматозоида, а жгутик расходует значительную часть АТР для движения.

а) Приняв, что реакция утилизации АТР в любой точке жгутика имеет нулевой порядок и что АТР распределен в промежуточном отделе равномерно в концентрации с₀, покажите, что изменение концентрации АТР в жгутике может быть описано уравнением с = 1—z(1 + ^—2/2) + ^—2z²/2, где — — модуль Тила жгутика, z — безразмерный параметр, характеризующий расстояние от жгутика, и с — безразмерный параметр, характеризующий концентрацию.

б) Каждый движущийся сперматозоид потребляет кислород для движения со скоростью 3,7—5,0∙10^-18 моль/с. С помощью указанных ниже дополнительных данных вычислите минимальное содержание АТР в сперматозоиде, необходимое для поддерживания его транспорта в жгутик за счет диффузии.

Коэффициент диффузии АТР (определенный с учетом содержания воды

в жгутике и извилистости) 3,6∙10^-6 см²/с

Объем промежуточного отдела 1,3∙10^-12 см³

Длина жгутика 5∙10^-3 см

Площадь поперечного сечения жгутика (без учета оболочки н фибрилл)

Выход АТР в расчете на поглощенный О₂ 6%

в) Найдено, что в среднем в одном сперматозоиде содержится 200∙10^-18 моль АТР. Утверждалось, что от одной трети до половины всего АТР расходуется митохондриями клетки. Оцените результаты ваших расчетов в части «б» этой задачи с точки зрения необходимости (или необязательности) учета других, отличных от пассивной диффузии механизмов транспорта для обеспечения соответствующего распределения АТР из митохондрий, локализованных в промежуточном отделе. [Nevo А. С., Rikmenspoel R., Diffusion of АТР in Sperm Flagella, J. Theoret. Biol., 26, 11 (1970).]

6.7. Теория мишени. Чтобы объяснить с молекулярно-биологической точки зрения потерю активности спорами, вирусами или клетками, была предложена гипотеза, согласно которой «в каждой клетке и в каждом организме существует ряд «мишеней» и изменение активности является результатом неупорядоченного поражения этих мишеней». (Smith J. М., Mathematical Ideas in Biology, p. 87, Cambridge University Press, London, 1971.) Рассмотрим следующую ситуацию.

Предположим, что содержащая N мишеней клетка облучена дозой К частиц. Пусть вероятность поражения данной мишени данной частицей равна р; очевидно, что величина р очень мала.

Вероятность того, что данная мишень не будет поражена данной частицей, равна 1—р.

Отсюда следует, что вероятность того, что данная мишень не будет поражена ни одной из К частиц, составляет

(1 — р)^K ≈ е^-Кр

а) Учитывая, что при большом К и малом р Кр≈ (К-1)p≈(К—2)р, докажите справедливость указанного приближения для этого типичного случая (большое К, малое р).

б) Покажите, что если относительное количество поврежденных клеток (под повреждением здесь подразумевается, что клетка поражена один раз или более) невелико, то «относительное количество поврежденных клеток равно NKp, т. е. пропорционально дозе». Если же, напротив, осталось мало неповрежденных клеток, то доля s последних определяется выражением ln s= -NKp; подтвердите справедливость этого уравнения.

в) Если клетка повреждается только после нескольких поражений, то для анализа такой ситуации можно использовать аналогичный подход. «Бактерия поражается идентичными бактериофагами; число поражающих одну бактерию бактериофагов равно r, каждый бактериофаг содержит N существенных генов. Жизнеспособный бактериофаг может образовываться путем рекомбинации при условии, что в каждом из N локусов один ген не поврежден» (см. приведенную выше ссылку). Покажите, что если «вероятность непоражения каждой мишени мала», то In s =Nln r — NpK (здесь под мишенями подразумевается число копий бактериофага r в клетке в момент облучения).

г) Покажите, что результаты предыдущего упражнения 6в согласуются с данными, изображенными графически на рис. 6У7.1,а; оцените все возможные параметры. Какие явления могут обусловливать поведение системы, графически представленное на рис. 6У7.1.6?

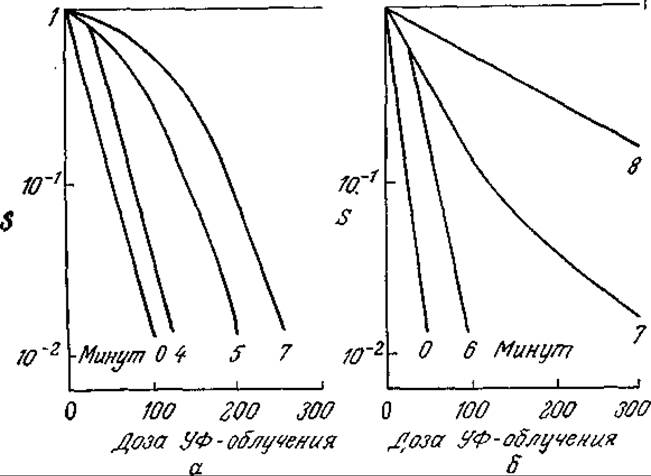
РИС. 6У7.1. Экспериментальная зависимость заражаемости S бактерий бактериофагом Т7 (а) и бактериофагом Т2 (б) от дозы облучения при различной продолжительности периода между заражением и облучением. [По материалам статьи: Benzer S., Resistance to Ultraviolet Light as an Index to the Reproduction of Bacteriophage, J. Bacteriol., 63, 59 (1952).]

6.8. Судьба мутантного гена в растущей популяции. В популяциях мутации происходят часто. Жизнеспособность мутантных организмов поразительно высока, а устойчивость мутантных генов низка. Для размножающейся половым путем популяции N диплоидных организмов в момент появления мутантного гена (аллеля) частота мутации равна 1/2N. Общее число организмов в популяции N превышает число организмов, участвующих в размножении N_e.

а) Для селективно нейтральной мутации (когда мутант не имеет ни преимуществ, ни недостатков по сравнению с исходным штаммом) среднее число поколений, предшествующих исчезновению мутантного гена, определяется выражением tl = 2(N_e/N)ln2N, а среднее число поколений, предшествующих закреплению гена (т. е. состоянию, когда частота гена равна 1,0) составляет t_f = 4N_e. Здесь величины t_lи t_f усреднены только по параметрам исчезновения и закрепления гена соответственно. Приняв N_e/N=0,5 и время

удвоения равным 1 ч, вычислите t_l и t_f для популяции с концентрацией 10⁷ клеток в 1 мл при объеме культуры 1 л.

б) Разброс значений t_f мал, а значений t_l велик по отношению к их средним величинам; этот факт вы можете подтвердить расчетом, взяв за основу следующие выражения:

в) Вероятность закрепления мутации в популяции можно оценить с помощью уравнения

где s₁ — селективное преимущество мутантного гена по сравнению с исходным геном. Покажите, что для типичных условий популяции микроорганизмов u=2s₁N_e/N. Следовательно, даже если селективное преимущество велико (s₁ = 1 % = 10^-2), вероятность того, что мутант в конце концов станет доминирующим в данной популяции, невелика (Kitnura М., Ohta Т., Theoretical Aspects of Population Genetics, Princeton University Press, Princeton, N.J., 1971).

6.9. Естественный отбор. Относительную приспособленность w данного генотипа x можно определить как отношение выживаемости генотипа х к выживаемости среднего генотипа популяции. (Под выживаемостью понимают отношение числа организмов, участвующих в размножении, к числу родившихся в каждом поколении.) Предположим, что приспособленность генотипа x линейно зависит от среднего выражения фенотипа так, что где а — мера интенсивности влияния разности на w(x) (а > 0). По определению g(x)—нормализованное распределение исходного генотипа [ʃ g(x)dx=1,0]. Через одно поколение распределение становится иным: g'(x) = w(x)g(x).

а) Выpазите через среднее значение и генетическую дисперсию σ². [Напомним, что среднее а дисперсия

б) Покажите, что в одном поколении изменение пропорционально 0% т. е. «скорость эволюции пропорциональна генетической дисперсии популяции» (основная теорема естественного отбора; см. работу: Wilson Е. О., Bossert W. Н., Primer of Population Biology, pp. 79—83, Sinauer Associates, Stamford, Conn., 1971).

в) Уилсон и Боссерт утверждают, что величина «некоторым образом пропорциональна дисперсии генотипа», даже если w нелинейно зависит от x. Выберите ряд обоснованных зависимостей w = f(x) и покажите справедливость (или некорректность) этого утверждения.

6.10. Кратные сайты оператора; регуляция промотора λР_R. Белок-репрессор промотора фага λP_R может связываться с тремя различными сайтами оператора, обозначенными символами O_R1, O_R2 и О_R3. Как показано на рис. 6У10.1, связывание репрессора с любым сайтом (за исключением O_R3) блокирует промотор P_R. Допустим, что реакция связывания репрессора с оператором равновесна и что константы равновесия реакций связывания репрессора с тремя сайтами составляют К₁, К₂ и К₃ соответственно.

а) Найдите общее уравнение, выражающее доступную для связывания с РНК-полимеразой долю промоторов P_R через константы равновесия, общее количество белка-репрессора и последовательности P_RO_R в клетке.

б) Оцените долю доступных промоторов в клетке, содержащей 25 последовательностей P_RO_R и 70 молекул репрессора. Примите К₁, К₂ и К₃ равными 125∙108, 1,25∙108 и 1∙10⁹М-1 соответственно. Каков физический смысл полученного вами результата?

РИС. 6У10.1. Относительные положения промотора P_R и трех операторов О_R1, О_R2 и О_R3 в фаге λ.

в) Решение предыдущих упражнений основывалось на принципах классической термодинамики. Статистическая термодинамика позволяет точнее оценить взаимодействия небольшого числа различных молекул в популяции клеток. Найдите решения задач 6.10а и 6.106 в свете теории, изложенной в статье: Berg О. G., Blomberg С., Mass Action Relations in vivo with Application to the Lac Operon; J. Theoret. Biol., 67, 523 (1977).

6.11. Скорости репликации ДНК в прокариотах и эукариотах, а) Для осуществления репликации необходимо расплетание двойной спирали ДНК. Предположим, что в ДНК имеются два центра расплетания (две репликационные вилки). Определите скорость вращения в центрах расплетания (в числе оборотов в минуту) ДНК Е. coli, если вся хромосома синтезируется за 41 мин. б) Период 5 линии клеток млекопитающих с геномом, содержащим 1,1 м двухцепочечной ДНК, длится 4,8 ч. Если по скорости синтеза ДНК эти клетки не отличаются от Е. coli, сколько репликационных вилок должно функционировать одновременно?

6.12. Рекомбинация фрагментов ДНК. Две двухцепочечные молекулы ДНК, 1 и 2, расщеплены рестрикционной эндонуклеазой EcoRI; одна цепь каждой из этих ДНК изображена ниже. Образовавшиеся фрагменты смешаны, рекомбинированы и обработаны ДНК-лигазой, катализирующей образование ковалентных связен. Перечислите все возможные продукты реакций.

6.13. Карты рестрикции. Относительные положения сайтов рестрикции во фрагментах ДНК определяют путем их частичного или полного расщепления рестриктазами и последующей оценки молекулярных масс образующихся фрагментов методом электрофореза в геле. Фрагмент ДНК Hind. IІІ, содержащий 3000 пар оснований, обработан EcoRI, ВglII и смесью этих ферментов. Электрофорез в геле показал, что при этом образуются два фрагмента, содержащие 1400 и 1600 пар оснований, три фрагмента с 400, 900 и 1700 парами оснований и четыре фрагмента с 400, 500, 900 и 1200 парами оснований соответственно. Определите карту рестрикции Hind III.

6.14. Праймер для кДНК интерферона. Для обеспечения максимальной вероятности клонирования кДНК, кодирующей аминокислотную последовательность интерферона из фибробластов (IFN-ß), полезно воспользоваться олиго дезоксирибонуклеотидным праймером, комплементарным 5'-концевой кодирующей последовательности мРНК. N-Концевая последовательность белка выражается формулой Met—Ser—Tyr—Asn. Перечислите все возможные соответствующие нуклеотидные последовательности мРНК и набор отвечающих им праймеров. Будьте внимательны при идентификации 3'- и 5'-концов в каждом из праймеров.

6.15. Продуцирование внутриклеточных белков рекомбинантными клетками. Оценка емкости биореактора, необходимой для продуцирования определенного количества аккумулирующегося в клетках продукта экспрессии клонированного гена, не представляет затруднений. Предположим, что рекомбинантный штамм Е. coli аккумулирует чужеродный белок, продукт экспрессии плазмидного гена, в концентрации до 30% от общего белка клетки. Если максимально допустимая плотность клеток равна 10⁹ клеток/мл, сколько белка можно выделить из 1 л объема биореактора?

Литература

Каждая из работ, указанная в гл. 1 и 2, содержит ценные сведения, имеющие непосредственное отношение к той или иной теме настоящей главы. Кроме того, рекомендуется следующая литература:

1. Стент Г. С., Кэлиндар Р., Молекулярная генетика. — М.: Мир, 1981. Прекрасно описаны основные понятия молекулярной генетики в историческом аспекте; особое внимание уделено подтверждению принятых в настоящее время гипотез.

2. Lewin В., Genes, 2d ed., John Wiley and Sons, New York, 1985. Хорошо изложенный, очень подробный и глубокий обзор, посвященный природе генов, их репликации и функциям.

3. Алберте Б., Брэй Д., Льюис Дж., Рафф М., Робертс К., Уотсон Дж. Д., Молекулярная биология клетки, т. 1—5. — М.: Мир, 1986—1987. Биология клетки, изложенная с точки зрения молекулярной биологии, представлена как одна из самых интересных отраслей биологических наук.

Введение в проблемы мутагенеза и прикладную генетику (с точки зрения микробиологической промышленности) дается в следующей литературе:

4. Eiander R. Р., Applications of Microbial Genetics to Industrial Fermentation, in Fermentation Advances, Perlman D. (ed.), Academic Press, Inc., New York, 1969.

5. Demain A. L., Overproduction of Microbial Metabolites and Enzymes Due to Alteration of Regulation, Adv. Biochem. Eng., 1, 113 (1971).

6. Dobrazanski W. T., Microbial Genetics in Pharmacy, Chem. Br., 10, 386 (1974).

7. Biology of Industrial Microorganisms, Demain A. L., Solomon N. A. (eds.), Benjamin Cummings and Co., Menlo Park, CA, 1984. В этом недавно опубликованном сборнике суммированы данные о метаболизме, системах регуляции и генетике микроорганизмов, используемых в настоящее время в промышленности. Одна из очень немногих книг, в которых детально рассмотрена микробиология плесеней и Streptomyces.

В приведенных ниже статьях рассмотрены гибридомы и методы слияния клеток, применяемые при синтезе моноклональных антител:

8. Peberdy J. F., Protoplast Fusion — A Tool for Genetic Manipulation and Breeding in Industrial Microorganisms, Enzyme and Microbial Tech., 2, 25 (1980).

9. Milstein C., Monoclonal Antibodies, Scientific American, 243, 66 (1980).

10. Boyd J. E., James K., McClelland D. B. L., Human Monoclonal Antibodies — Production and Potential, Trends in Biotech., 2, 70 (1984).

Отдельные примеры практического применения генетики микроорганизмов рассмотрены в следующих статьях из сборника Fermentation Advances, Pertman D. (ed.), Academic Press, Inc., New York, 1969:

11. Pardee A. B., Enzyme Production by Bacteria, p. 3.

12. Veda К., Some Fundamental Problems of Continuous L-Glutamic Acid Fermentations, p. 43.

13. Furuya A., Misawa M., Nara T., Abe S., Kinoshita S., Metabolic Controls of Accumulations of Amino Acids and Nucleotides, p. 177.

В связи с ростом научных и технических достижений в последние годы публикуется все больше работ, посвященных технологии рекомбинантных ДНК.

В приведенном ниже перечне они расположены по возрастающей степени сложности — от вводных, общих обзоров до подробного описания методов и результатов исследований.

14. Cohen S. N., The Manipulation of Genes, Scientific American, 233, 24 (1975).

15. Gilbert W., Villa-Komaroff L., Useful Proteins from Recombinant Bacteria, Scientific American, 242, 74 (1980).

16. Wetzel R., Applications of Recombinant DNA Technology, American Scientist, 68, 664 (1980).

17. Watson J. D., Tooze J., Kurz D. T., Recombinant DNA: A Short Course, W. H. Freeman and Co., New York, 1983.

18. Glover D. M., Genetic Engineering: Cloning DNA, Chapman and Hall, New York, 1980.

19. Old R. WPrimrose S. B., Principles of Gene Manipulation, 2d ed., University of California Press, Berkeley, 1981.

20. Rodriguez R. L., Tait R. C., Recombinant DNA Techniques: An Introduction, Addison-Wesley Publishing Co., Reading Massachusetts, 1983.

21. Recombinant DNA, Methods in Enzymology, vols. 68 (1979), 100, 101 (1983), Academic Press, New York.

22. Sanger F., Nicklen S., Coulson A. R., DNA Sequencing with Chain-Terminating Inhibitors, Proc. Natl. Acad. Sci. USA, 74, 5463 (1977).

23. Gray P. W. et al., Expression of Human Immune Interferon cDNA in E. coli and Monkey Cells, Nature, 295, 503 (1982).

Научные и общественные дискуссии, посвященные технологии рекомбинантных ДНК, отражены в книге:

24. Watson J. D., Tooze J., The DNA Story, W. M. Freeman and Co., San Francisco, 1981.

Работы, посвященные изучению клеточных циклов вообще и циклов Е. coli

и S. cerevisiae в частности, обобщены в следующей литературе:

25. Mitchison J. М., The Biology of the Cell Cycle, Cambridge University Press, London, 1971.

26. Ingraham J. L., Maalee O., Neidhardt F. C., Crowth of the Bacterial Cell, Sinauer Associates, Inc., Sunderland, Massachusetts, 1983.

27. Hartwell L. H., Saccharomyces cerevisiae Cell Cycle, Bad. Rev., 38, 164 (1974).

28. Lievense J. C., Lim H. C., The Growth and Dynamics of Saccharomyces cerevisiae, in Annual Reports on Fermentation Processes, vol. 5, p. 211, Tsao G. T. (ed.)., Academic Press, New York, 1982.