Биохимия - Химические реакции в живой клетке Том 1 - Д. Мецлер 1980
Как молекулы соединяются друг с другом
Кооперативные изменения конформации
Равновесия связывания для димеризующегося белка
Все описанные в уравнениях (4-42) — (4-48) равновесные процессы, в ходе которых образуются димеры А2, AB и В2 или к димеру присоединяется одна или две молекулы X, представлены схематически на рис. 4-16. Над каждой стрелкой приведена характеризующая эту стадию микроскопическая константа, умноженная на соответствующий
статистический множитель. Степень насыщения 
задается следующим уравнением:
Каждый из девяти слагаемых в числителе представляет собой концентрацию одного из девяти комплексов, содержащих X (рис. 4-16). Четырнадцать слагаемых в знаменателе — это концентрация белка в каждой из форм (включая те, которые не содержат X). Приведенные концентрации белка соответствуют молекулярному весу димеров, в связи с чем некоторые члены знаменателя умножены на 1/2.
Все члены числителя и знаменателя уравнения (4-49) можно выразить через [X], используя микроскопические константы, приведенные на рис. 4-16. Для этого надо составить уравнение [аналогичное уравнению (4-15)], связывающее у с [X], KAX и КBX, Ktи с константами взаимодействия КAA, КAB и KBB. Поскольку такое уравнение в общем виде очень громоздко, рассмотрим некоторые частные случаи, когда оно имеет более простой вид.
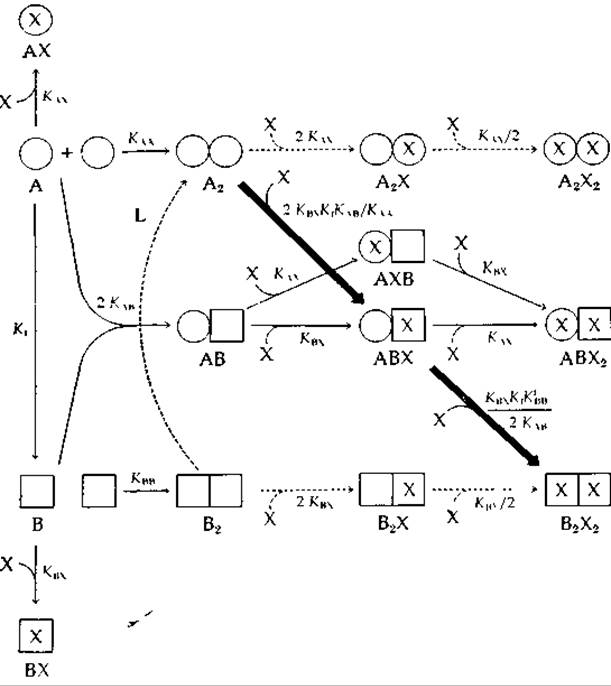
РИС. 4-16. Возможные формы димеризующихся белков, существующих в двух конформационных состояниях; в каждом протомере имеется один центр связывания с лигандом X. Пунктирными стрелками указаны равновесные процессы, рассмотренные Моно, Уайменом и Шанжё, а сплошными — Кошландом и др. [61, 62]. Жирные стрелки относятся к простейшей модели индуцированного соответствия, не учитывающей диссоциации димера. (Заметим, что, хотя все стрелки имеют только одно направление, соответствующие процессы обратимы.) Величины КAX и КBX считаются одинаковыми для всех субъединиц независимо от того, в какой форме они находятся — в мономерной или димерной.
а. Диссоциация олигомеров отсутствует
Если обе константы — КАА и КВВ — достаточно велики, то диссоциация на мономеры происходить не будет. Тем не менее переход между конформациями А и В внутри димера или олигомера более высокого порядка все-таки может осуществляться и математические соотношения, приведенные на рис. 4-16, остаются применимыми. Для описания наиболее распространенных моделей олигомерных ферментов необходимо ввести дальнейшие упрощения.
1. Модель Моно—Уаймена—Шанжё [33]. Если принять, что образуются только симметричные димеры, т. е. КАА и КВВ≫КАВ [уравнениє (4-45)], то можно ограничиться рассмотрением лишь тех равновесных процессов, которые обозначены на рис. 4-16 пунктирными стрелками. В отсутствие лиганда X отношение [В2]/[А2] =const [1/L в обозначениях Моно—Уаймена—Шанжё; см. также уравнение (4-45)]:
На положение равновесия влияют как константы ассоциации КАА и КВВ, так и константа перехода Кt. Отношение [В2] к [А2] может быть мало, если Каа и АВВ близки, a Кt невелика. Если Кt ≃ 1, это отношение тоже может быть мало при условии, что КАА≫КВВ, т. е. когда в комплексе А2 субъединицы связаны прочнее, чем в В2. Для этого случая уравнение (4-49) упрощается и принимает следующий вид:
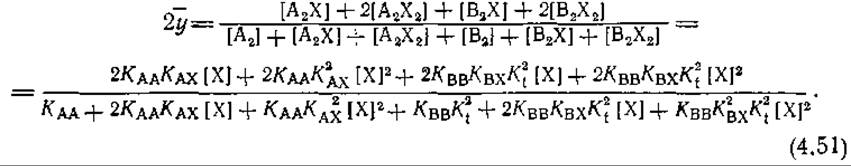
Подставляя выражение для 
из (4-50) в (4-51), получаем
В случае олигомера из п субъединиц Моно и др. делают допущение о том, что все центры связывания в данном конформере независимы и равноценны. Уравнение для 
вытекающее из (4-29), имеет в этом случае следующий вид:
Первоначально мы предполагали, что В2 связывается с X прочнее, чем А2. Следовательно, если равновесие в уравнении (4-50) сильно смещено в сторону образования В2 (L мало), то добавление X не повлияет на равновесие между двумя конформерами и связывание будет некооперативным. Уравнение (4-53) сводится в этом случае к (4-30). Если, однако, равновесие смещено в сторону образования А2 (L велико), то добавление X приведет к сдвигу равновесия в сторону образования В2 (который прочнее связывается с X). Более того, поскольку выражение для у (4-52) содержит в знаменателе член К2ВХ [X]2, связывание начнет становиться кооперативным. В предельном случае, когда L велико и КАХ ≃ 0, большинство членов в уравнении (4-62) станет равным 0 и оно примет вид приведенного ранее уравнения (4-33), относящегося к случаю полностью кооперативного связывания, когда К = К2ВХ L. При других значениях KAX, KBX и L наблюдается неполная кооперативность [60].
Модель индуцированного соответствия Кошланда [61, 62]’ В этой модели рассматриваются только формы А2, АВХ и В2Х2 (жирные стрелки на рис. 4-16). Выражение для 
имеет следующий вид1:
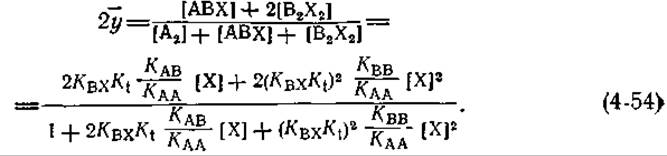
Если величина КАВ мала (нет «смешанного» димера), это выражение также сводится к уравнению (4-33), описывающему полностью кооперативное связывание, причем 
определяется в этом случае следующим образом:
Если же КАВ много больше КАА и КВВ, то будет иметь место антикооперативность (отрицательная кооперативность). В этом случае кривая насыщения, как и кривая связывания протонов дианионом сукцината (рис. 4-4), будет двухступенчатой.
б. Случай, когда в одной из конформаций белок диссоциирует
Рассмотрим случай, когда константа КBB очень мала и В2 легко диссоциирует на мономеры. Тогда присоединение X приведет к диссоциации димера. Хорошо известным примером белка такого рода может служить гемоглобин миноговых, который представляет собой димер и после связывания кислорода диссоциирует на мономеры [64]. В этом случае уравнение (4-49) сводится к такому виду:
Читателю предоставляется интересная возможность проанализировать, можно ли на основании этого уравнения предсказать слабое кооперативное связывание кислорода гемоглобином миноговых.
Посмотрите еще раз на выражение для константы L, определяющей отношение между количествами белка, находящегося в конформациях А и В в отсутствие лиганда. Из уравнения (4-50) следует, что L может достигать больших значений (преимущественно присутствует конформер А) либо при очень малой Kt, либо при КВВ≪КАА. Так, если Кt≃1 и L велико, это означает, что связь между субъединицами в В2 значительно слабее, чем в А2, и вполне возможно, что присоединение X приведет к диссоциации молекулы, как это имеет место в случае гемоглобина миноговых. Если же Ktмала (это означает, что молекулы белка находятся преимущественно в конформации А за счет большей стабильности этой формы), КВВ может быть значительно больше, чем КАА, если КАА при этом достаточно мала, димер А2 полностью диссоциирует. Присоединение лиганда приведет к ассоциации и кооперативному связыванию. Это можно легко показать, выписав соответствующие члены из уравнения (4-49).
1 Иногда Кошланд произвольно принимает КАА = 1, считая, что КВВ — это константа взаимодействия, равная КВВ/КАА. Хотя это условие и упрощает алгебраические преобразования, оно правомерно лишь в случае полностью ассоциированных систем, поэтому в данной книге мы будем пользоваться константами, определяемыми уравнениями (4-46) — (4-48).