Химия белка. Структура, свойства, методы исследования - Шендрик А.Н. 2022
Методы экспериментального исследования структуры белков
Рентгеноструктурный анализ
Дифракция рентгеновских лучей на кристаллах
Длина волны генерируемого в рентгеновских трубках электромагнитного излучения составляет 0.2 - 2 А. Эти значения как раз соответствует величинам межатомных расстояний в молекулах. К сожалению, мы пока не умеем фокусировать рентгеновские лучи. Не знаем как и не умеем создавать для них линзы. Следовательно, мы не можем построить микроскоп, использующий рентгеновские лучи. По этой собственно причине рентгеноструктурное исследование не позволяет получить непосредственное изображение объекта, а дает лишь создаваемую им дифракционную картину. Последняя, как правило, весьма сложна даже для простых кристаллов. По мере увеличения числа атомов в элементарной ячейке, восстановление пространственной структуры объекта, породившего наблюдаемую в опыте дифракционную картину, становится задачей, неразрешимой без применения мощной вычислительной техники и надлежащего программного обеспечения.
Дифракцию рентгеновских лучей на кристаллах открыл Лауэ в 1912г. Он же описал условия появления дифракционной картины при рассеяниии рентгеновских лучей трехмерными кристаллами. В настоящее время, однако, более широко распространена более наглядная трактовка дифракционного эффекта, предложенная в 1914 г. Бреггом. Суть ее в следующем. Пусть мы имеем кристалл, в котором атомы расположены регулярным образом в плоскостях, отстоящих друг от друга на расстоянии d. По законам линейной оптики, падающие на эти две плоскости лучи, не будут гасить друг друга после отражения лишь в том случае, если разность их хода (разность путей пройденных лучами) будет кратной длине волны падающего излучения (см рис.)
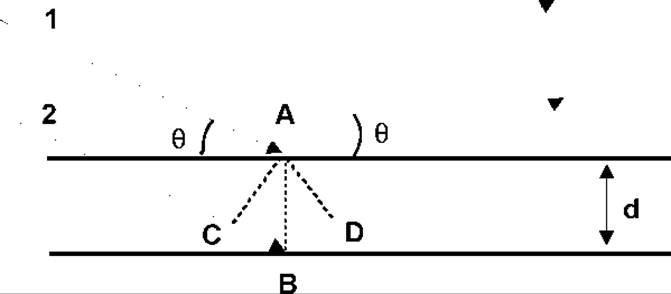
Как видно из рис. разность хода лучей 1 и 2 равна СВ + BD. Учитывая, что:
CB = BD = dsinθ,
условие появления интерференционного максимума для лучей 1 и 2 выразится следующим образом:
2dsinθ = nλ
где n- целое число 1,2,3... (порядок отражения)
Последнее соотношение и есть уравнение Брегга. Оно определяет то единственное значения угла 0, при котором отраженные от различных плоскостей трехмерного кристалла лучи не гасят друг друга. Все остальные, рассеянные под отличными от 0 углами, лучи при наложении взаимно ослабляются и гасятся, т.е. не дают интерференционной картины.
Очень существенными для понимания явления дифракции рентгеновских лучей на кристаллах являются следующие особенности взаимодействия этих лучей с веществом и закономерности их дифракции.
> Рассеяние рентгеновских лучей происходит на электронах.
> Показатель преломления рентгеновских лучей для обычных кристаллических веществ равен практически единице.
> Дифракционная картина кристалла формируется только в результате интерференции когерентных волн, т.е. только теми лучами, длина волны которых не изменилась после рассеяния.
> Интенсивности дифракционных максимумов (рефлексов) являются комплексными параметрами и объединяют в себе информацию как об интенсивности рассеянных лучей, так и об их фазах. Проще говоря по интенсивности рефлекса ничего нельзя сказать о том, на каких именно атомах кристалла рассеянны лучи, породившие данный конкретный дифракционный максимум. Этот так называемая фазовая проблема РСА. Без разрешения фазовой задачи, пространственные координаты атомов кристаллической решетки остаются неопределенными.
> Закон отражения рентгеновских лучей кристаллами имеет ту особенность, что зависимость между углом отражения (0) и величиной межплоскостного расстояния (d) является обратно пропорциональной (см.ур.Брегга): sinθ = nλ/2d.
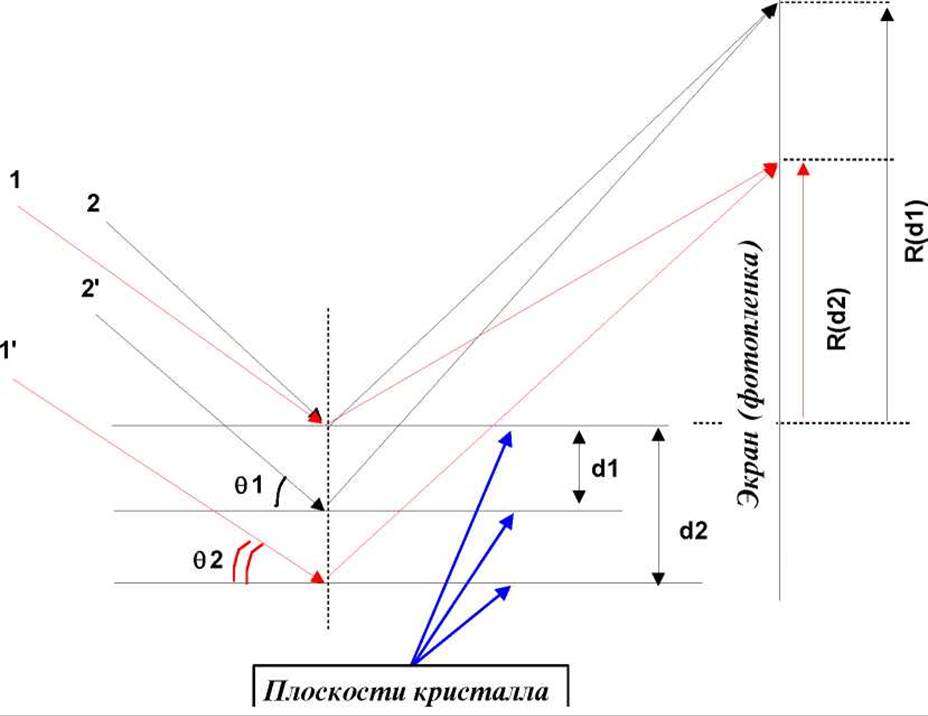
Это означает фактически, что дифракционные пятна (рефлексы) на рентгенограмме дают как бы обратную картину размещения атомов в кристалле. Иначе говоря, чем ближе расположены атомы (чем меньше межплоскостное расстояние) тем сильнее отклонится отраженный рентгеновский луч на рентгенограмме (см. рисунок выше.).
Этой особенностью дифракционной рентгенографии обусловлено введение в РСА пространства обратной решетки, а пространство, в котором расположена дифракционная картина называют обратным пространством. Абстрактно, это обратное пространство можно представить себе как совокупность дифракционных пятен (точек) существующих в пространстве, окружающем кристалл. Практически, все эти рефлексы фиксируют на фотопленке или посредством дифрактометра, вращая кристалл.
Преобразование от пространства кристаллической решетки к пространству обратной решетки есть просто строгая математическая формулировка брэгговского закона дифракции. При этом один масштабный параметр - расстояние от кристалла до фотопленки - выбирается произвольно.
Задача рентгеноструктурного анализа заключается в том, чтобы перейти от системы точек в обратном пространстве к искомой структуре решетки в прямом пространстве. Для простых молекул она решалась методом проб и ошибок. Известны были заранее симметрия и кристаллографические свойства кристалла, а также строение молекул, заполняющих решетку. Это давало возможность избегать многих ошибок и выбирать правильную структуру из немногих гипотетических альтернативных вариантов. При этом, кроме координат дифракционного пятна, имеется еще один важный фактор - интенсивность пятна. Так как рентгеновские лучи одинаково рассеиваются электронами каждого атома, то интенсивность отражения (I) от некоторой системы плоскостей будет определяться так называемым структурным фактором, равным сумме квадратов атомных номеров, т. е. чисел электронов всех атомов, на единицу площади:
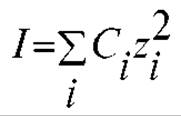
где Сі, — концентрация атомов i-го типа в единице площади, zi - атомный номер.
Сделав предположение о расположении атомов в решетке, легко рассчитать всю ожидаемую картину как по положению пятен, так и по интенсивности. Рентгеноструктурный анализ долгое время обходился этой примитивной техникой. Однако постепенно в поле зрения рентгеноструктурного анализа вошли сложные органические молекулы. И от простого подтверждения структурных формул неорганических и органических соединений рентгенография перешла к разгадке строения новых неизученных молекул. Пробным камнем для метода послужила молекула пенициллина, которая вследствие крайней химической лабильности долго не поддавалась усилиям химиков-органиков. Строение пенициллина было найдено, исходя из рентгеноструктурного анализа кристалла в работе Дороги Ходжкин (1944 г.). Это было первое применение рентгеновских лучей для решения задачи, перед которой методы органической химии отступили. Молекула пенициллина содержит 23 атома, кроме водородов.
Следующая по сложности задача, разрешенная той же исследовательницей, было определение структуры витамина В12. В этом случае необходимо было найти из рентгенограммы пространственные координаты 93 атомов, и это удалось осуществить. В итоге была сконструирована пространственная модель молекулы витамина, а следовательно, найдена его структурная формула, т. е. схема расположения ковалентных связей между атомами.
После этого пришла эра белков, и задача анализа структуры усложнилась неимоверно. В качестве первых объектов были избраны хромопротеиды гемоглобин и миоглобин, содержащие в своем составе гем-группу. РСА этих двух белков крови был выполнен Кембриджской школой.