Основы биоинформатики - Огурцов А.Н. 2013
Основания биоинформатики
Биологические последовательности
Точечная матрица сходства
Точечная матрица (dot plot) - это простейшее изображение, которое даёт представление о сходстве между двумя последовательностями.
Точечная матрица сходства (или совпадений) представляет собой таблицу или матрицу, в которой строки соответствуют элементам одной последовательности, а колонки - элементам другой последовательности. В простейшем варианте ячейки точечной матрицы оставляют пустыми, если сравниваемые элементы различны, и заполняются, если они совпадают. Совпадающие фрагменты последовательностей отображаются в виде диагоналей, идущих из верхнего левого угла в нижний правый.
Для примера построим точечную матрицу, показывающую совпадения между короткой строкой ПРОФЕССОРОГУРЦОВ и длинной ПРОФЕССОРАЛЕКСАНДРНИКОЛАЕВИЧОГУРЦОВ (рисунок 7).
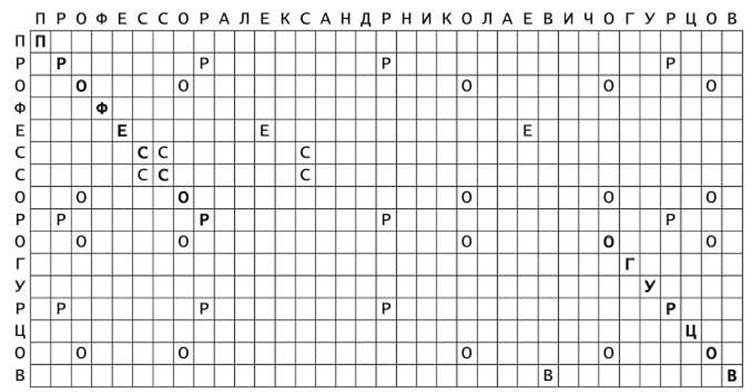
Рисунок 7 - Точечная матрица сходства двух строк
Буквы, соответствующие длинным совпадающим участкам, выделены жирным шрифтом, а одиночные совпадения, не выделены жирным шрифтом. Очевидно, выравнивание в этом случае будет иметь вид
![]()
На рисунке 8 представлена точечная матрица, показывающая как глобальные, так и локальные совпадения повторяющейся последовательности АБРАКАДАБРАКАДАБРА с самой собой.
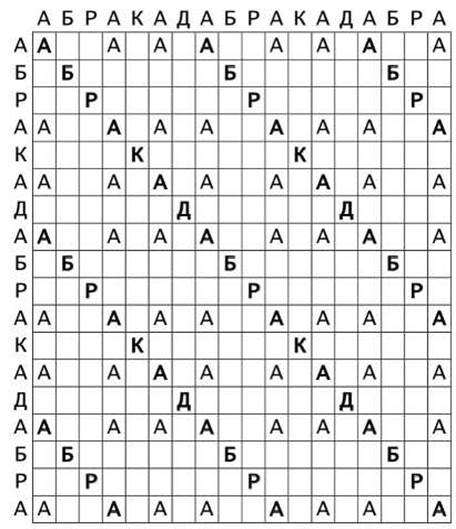
Рисунок 8 - Точечная матрица совпадений в повторяющейся последовательности
Вид точечной матрицы может наглядно показать наличие палиндромных последовательностей в анализируемой строке.
Так палиндромами являются сайты рестрикции в ДНК для рестрикционных ферментов (рисунок 9).
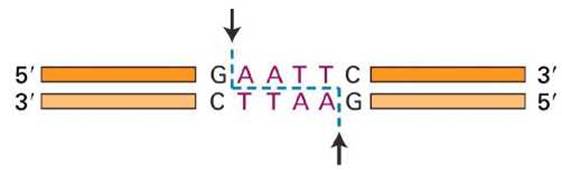
Рисунок 9 - Разрезание ДНК рестрикционным ферментом EcoRI
Иногда палиндромность ДНК-последовательности определяется тем, что с этим участком ДНК должен взаимодействовать димерный белок, одна субъединица которого взаимодействует с одним плечом палиндрома, а другая - с другим плечом на комплементарной цепи, как, например, в случае связи рецептора глюкокортикоидных гормонов с гормон-распознающим элементом (HRE) ДНК (рисунок 10).
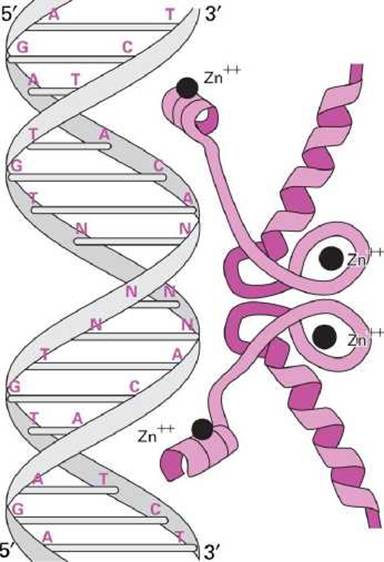
Рисунок 10 - Палиндромный гормон-распознающий элемент (HRE) ДНК, связанный с димеризованными рецепторами стероидных гормонов
HRE является палиндромом, то есть участком ДНК, обе нуклеотидные нити которого одинаковы, если каждую из них читать в направлении 5'→3' (см. [7], п. 3.5). Для нашего примера HRE имеет вид
![]()
Каждая из нитей HRE содержит 6-ти нуклеотидную последовательность AGAACA, которая называется core recognition motif. Поскольку HRE содержит два таких мотива, то к HRE присоединяются два рецептора.
Две 6-ти нуклеотидные последовательности разделены тремя парами оснований (обозначены NNN на рисунке 10), которые нужны для того, чтобы обеспечить достаточно пространства для того, чтобы гомодимер рецепторов мог связаться с HRE. Эти три пары оснований могут быть любыми, поскольку они не влияют на прочность связывания с рецепторным комплексом.
На рисунке 11 показан характерный вид точечной матрицы палиндрома АРОЗАУПАЛАНАЛАПУАЗОРА.
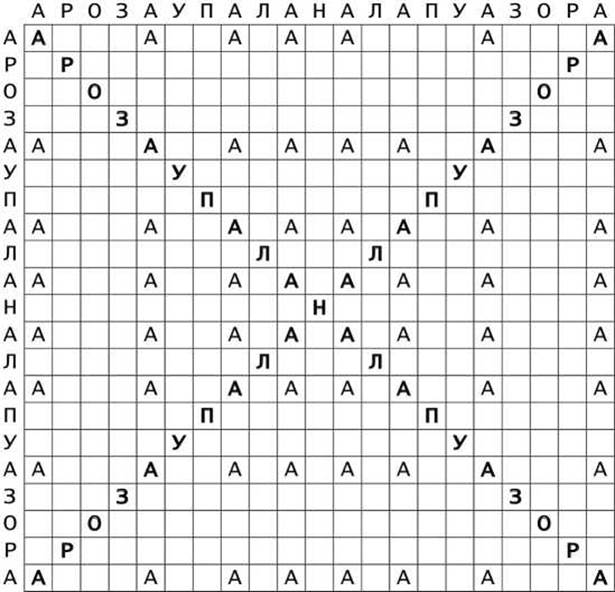
Рисунок 11 - Точечная матрица сходства (совпадений) для палиндромной последовательности АРОЗАУПАЛАНАЛАПУАЗОРА
Длинные участки ДНК или РНК, содержащие инвертированные повторы такого типа, могут формировать шпилечные структуры. Кроме того, некоторые подвижные элементы, выделенные из растений, содержат настоящие (неточные) палиндромные последовательности - инвертированные повторы некомплементарных последовательностей, расположенных на той же цепи.
Ещё один пример палиндрома - ttttcgtgagtgcggaggctttt - фрагмент генома вируса Wheat Dwarf Virus, вызывающего остановку роста пшеницы.
Точечная матрица позволяет быстро проиллюстрировать родство между двумя последовательностями. Яркие признаки сходства чётко проявляются. Например, точечная матрица, отображающая родство между генами митохондриальной АТФазы миноги Petromyzon marinis (lamprey) и морской собаки Scyliorbinus canicula (dogfish), показывает, что сходство между этими последовательностями менее всего выражено вначале (рисунок 12).

Рисунок 12 - Точечная матрица совпадений для АТФазы-6 из миноги и морской собаки
Иногда точечную матрицу строят в "традиционном" представлении, когда "начало координат" - точка начала последовательностей находится не в левом верхнем, а в левом нижнем углу. Соответственно изменяется и направление вертикальной оси (рисунок 13).
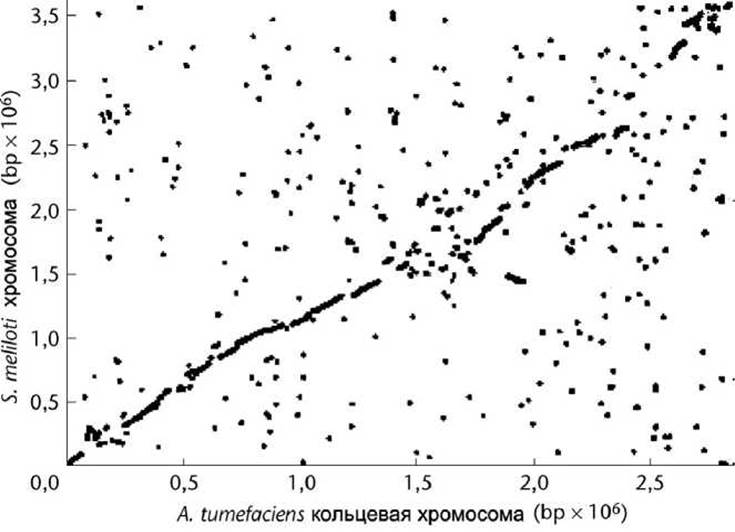
Рисунок 13 - Точечная матрица совпадений линейной хромосомы S. meliloti и кольцевой хромосомы A. tumefaciens
Рисунок 13 позволяет предположить, что у этих организмов был общий предок.
Еще один пример использования точечных матриц для сравнения нуклеотидных последовательностей в генах, кодирующих а и ß субъединицы гемоглобина человека, представлен на рисунке 14. Главная диагональ рисунка демонстрирует значительное подобие последовательностей.
Часто участки сходства могут быть смещены, а это приводит к тому, что они появляются на параллельных диагоналях точечной матрицы совпадений. Такие смещения происходят в результате вставок (инсерций) или удалений (делеций).
Пример на рисунке 7 демонстрирует результат вставки строки АЛЕКСАНДРНИКОЛАЕВИЧ внутрь строки ПРОФЕССОРОГУРЦОВ, или, что-то же самое, удаления подстроки АЛЕКСАНДРНИКОЛАЕВИЧ из строки ПРОФЕССОРАЛЕКСАНДРНИКОЛАЕВИЧОГУРЦОВ. Оба действия приводят к смещению диагональных совпадений от основной диагонали.
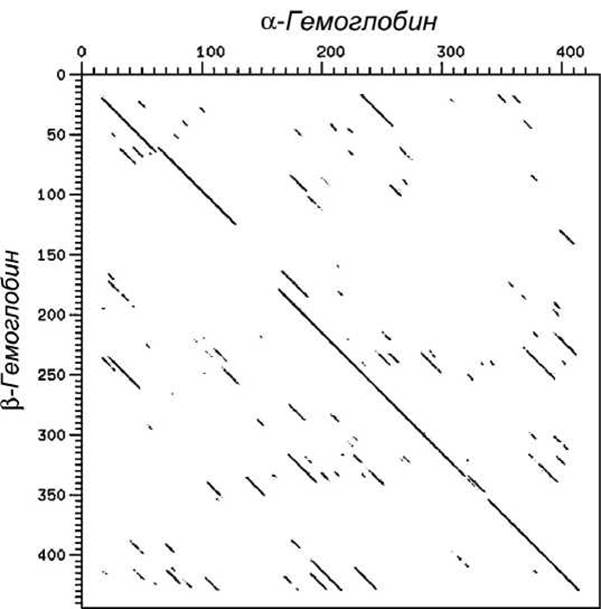
Рисунок 14 - Точечная матрица совпадений генов, кодирующих а и ß субъединицы гемоглобина человека
Для последовательностей нуклеотидов в генах, кодирующих а и ß субъединицы гемоглобина человека, также заметны смещения диагональной линии, свидетельствующие о наличии вставок или удалений в гемоглобиновых генах.
На рисунке 15 показана точечная матрица совпадений белков РАХ-6 из мыши и eyeless из плодовой мушки Drosophila melanogaster.

Рисунок 15 - Точечная матрица совпадений белков РАХ-6 из мыши (вертикальная ось) и eyeless из плодовой мушки Drosophila melanogaster (горизонтальная ось)
На рисунке 15 явно проявляются три продолжительных участка сходства. Два из них находятся в начале последовательностей, а третий — в середине. Между двумя из трех участков в последовательности белка из мыши есть более длинный промежуточный участок, чем в последовательности белка из плодовой мушки.
Сравнивая глобальное выравнивание, которое ищет подобие на всем протяжении последовательностей, и локальное выравнивание, которое сосредоточивается лишь на отдельных областях подобия в некоторых частях последовательностей, следует отметить, что с точки зрения биолога поиск локального подобия может дать более значимые и точные результаты, чем оценка выравнивания по всей длине последовательностей.
Это связано с тем, что функционально активные участки обычно расположены в пределах относительно коротких областей, которые остаются консервативными независимо от удалений или мутаций, происходящих в остальных частях последовательности.
Главное преимущество метода точечных матриц при поиске выравниваний последовательностей состоит в том, что он позволяет найти все возможные совпадения остатков между двумя последовательностями и предоставляет исследователю возможность выбора самых ценных из них. И уже затем могут быть определены последовательности хорошо выровненных областей - уже с помощью других методов выравнивания последовательностей (например, динамического программирования). Выравнивания, производимые этими программами, могут быть сопоставлены с выравниванием по точечной матрице; такое сличение покажет, совпадают ли самые длинные области и расположены ли вставки и удаления в наиболее подходящих местах.
Точность определения совпадающих областей может быть повышена за счёт отфильтровывания случайных совпадений, найденных в точечной матрице. Фильтрация выполняется с помощью скользящего окна, позволяющего сравнивать эти две последовательности одновременно.
Идентификацию выравниваний последовательностей с помощью метода точечных матриц можно проводить путём подсчёта точек на всех возможных диагоналях матрицы (чтобы определить статистически, какие диагонали дают больше всего совпадений) и последующего сравнения счётов этих совпадений с результатами произвольного сравнения последовательностей.
Анализ точечной матрицы - это, прежде всего, метод сравнения двух последовательностей с целью поиска возможного выравнивания элементов этих последовательностей. Кроме того, к этому методу обращаются для предсказания комплементарных участков в составе РНК, которые могут участвовать в формировании вторичной структуры РНК (например, шпилек) и при поиске прямых или обратных повторений в последовательностях белков и ДНК.
Так, например, могут быть обнаружены повторные области, распределённые по всей длине, как отдельных хромосом, так и всего набора хромосом.
Для примера, на рисунке 16 представлена точечная матрица сравнения геномов Sorghum bicolor и Otyza Sativa.
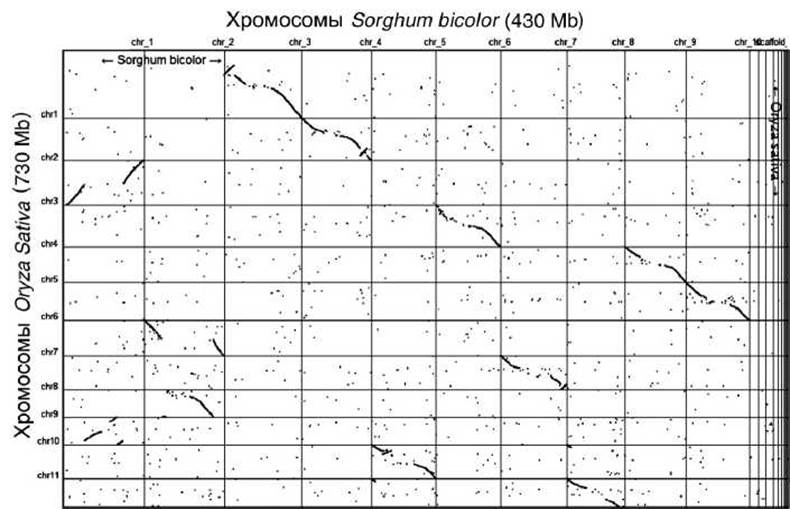
Рисунок 16 - Точечная матрица совпадений геномов Sorghum bicolor и Oryza Sativa; Mb - мегабэйзы - миллионы пар оснований
Параллельно диагонали, идущей из левого верхнего угла в правый нижний, расположены прямые совпадения в одинаковых нитях ДНК геномов. А параллельно диагонали, идущей из правого верхнего угла в левый нижний, расположены обратные повторения в комплементарных нитях ДНК (инверсные повторы между геномами).
Так, например, наблюдается как значительное прямое сходство между хромосомой 2 О. sativa и хромосомой 4 S. bicolor, так и наличие инверсного участка. А для хромосомы 1 S. bicolor и хромосомы 3 О. sativa наблюдаются только два инверсных участка.
Таким образом, метод точечных матриц наглядно демонстрирует любые возможные выравнивания последовательностей в виде диагоналей матрицы. Анализ точечной матрицы может легко показать присутствие вставок или удалений, а также прямых и обратных повторений, которые гораздо труднее найти другими, пусть даже более автоматизированными методами.
Точечная матрица не просто визуализирует сходство двух последовательностей, она вообще демонстрирует все возможные выравнивания и отображает их относительное качество.
Выравнивание не должно изменять "смысл" последовательностей, поэтому при выравнивании должна сохраняться последовательность символов в строке и не должно быть перестановок символов. Поэтому при построении выравнивания, начиная с верхнего левого угла точечной матрицы, разрешены только три типа шагов:
1) строго направо (→);
2) строго вниз (↓);
3) по диагонали слева направо и сверху вниз (↘).
Любой путь по точечной матрице от левого верхнего угла к правому нижнему углу, построенный с помощью этих шагов, соответствует одному из возможных выравниваний.
Например, на рисунке 17 приведены три варианта выравнивания строк АЛЕКСАНДРНИКОЛАЕВИЧОГУРЦОВ и АЛЕКСАНДРОГУРЦОВ:

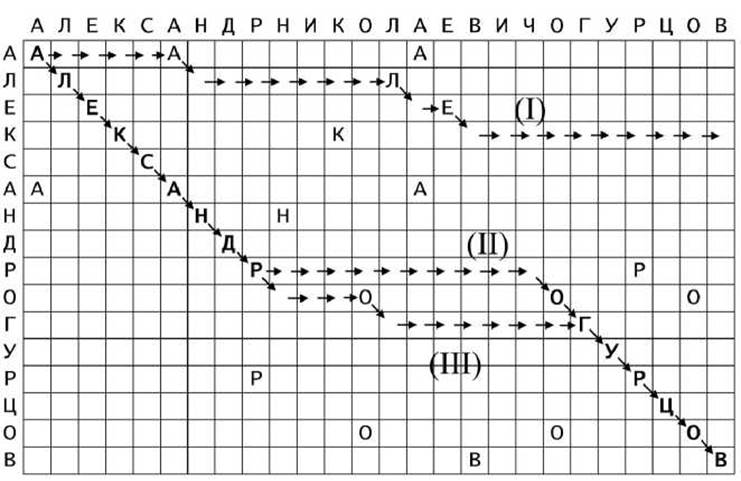
Рисунок 17 - Возможные варианты выравнивания
Любой путь по точечной матрице от верхнего левого угла к нижнему правому проходит последовательность ячеек, каждая из которых предсказывает пару позиций: одну из ряда и одну из столбца, которые совпадают с выравниванием; либо означают пробел в одной из последовательностей. Путь не обязательно должен проходить лишь заполненные позиции. Тем не менее, чем больше заполненных позиций, на диагональном отрезке пути, тем больше совпадающих остатков в выравнивании.
Если направление движения между последующими ячейками диагональное, то пара следующих друг за другом сравниваемых остатков оказываются в выравнивании без вставки между ними (сопоставляются).
Если направление движения горизонтальное, то в последовательность, служащую указателем рядов, вставляется пропуск.
Если же направление движения вертикальное (вниз), то пропуск вставляется в последовательность, индексирующую столбцы.
Следует обратить внимание на то, что ни одно движение не может совершаться вверх или влево, так как это соответствовало бы сравнению нескольких остатков одной последовательности со всего лишь одним остатком другой. Математическая интерпретация изложенного выше способа выбора пути по точечной матрице основывается на представлении пути выравнивания в виде графа.
Граф определяется как совокупность множества вершин (или узлов) и множества связей между узлами, которые называются рёбра (или дуги).
Ориентированный граф (кратко орграф) - это (мульти) граф, рёбрам которого присвоено направление.
Маршрутом в орграфе называют чередующуюся последовательность вершин и дуг (вершины могут повторяться). Длина маршрута - это количество дуг в нем.
Путь - это маршрут в орграфе без повторяющихся дуг; простой путь - без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой.
Рассмотрим две последовательности длиной m и n. Выравниванием этих последовательностей будет ориентированный граф G с узлами (i, j) (0 ≤ i ≤ m, 0 ≤ у ≤ n) решётки размером (m + 1) х (n + 1). Ребро графа от узла (i, j) к узлу (i', j') возможно только если 0 ≤ i' - i ≤ 1 и 0 ≤ j' - j ≤ 1.
На рисунке 18 представлен граф выравнивания для последовательностей Х= gtccgtg и Y= atactgg, в котором существуют вертикальные, горизонтальные и диагональные рёбра.

Рисунок 18 - Граф выравнивания последовательностей gtccgtg и atactgg
В ориентированном графе концом графа (или стоком, sink) является узел, к которому направлены все прилегающие рёбра, а началом графа (или источником, source) является узел, от которого направлены все прилегающие рёбра. В графе глобального выравнивания единственным началом (source) является узел (0,0), а единственным концом графа (sink) выравнивания является узел (m, n).
Выделенный жирными стрелками путь на графе выравнивания (рисунок 18) можно представить в виде
![]()
где s — начало (0,0). Соответствующее выравнивание будет иметь вид
![]()
Другой способ интерпретации пути по точечной матрице - это порядок редактирования (edit script). Он представляет собой указание серий операций, которые трансформируют последовательность, индексирующую столбцы, - горизонтально расположенную последовательность (над таблицей) - в последовательность, которая индексирует ряды, - вертикально расположенную последовательность (слева от таблицы).
Каждое движение говорит нам о проведении одной из операций — замены, вставки или делеции (удаления). По достижении конца пути получится преобразование одной последовательности в другую.
Вообще говоря, несколько различных последовательностей редакционных операций могут преобразовать одну последовательность в другую за одно и то же количество шагов, при этом, однако, они могут соответствовать различным выравниваниям.
Для того чтобы количественно сравнивать результаты различных вариантов выравнивания, операциям редактирования сопоставляется определённая схема оценок. Эти схемы могут быть очень простыми, как, например, (+1 балл) за каждую пару совпадающих знаков (замена) и штраф (-1 балл) за несовпадение.
Штрафы могут быть фиксированными, пропорциональными и линейными, складывающимися из штрафа за введение пропуска и дополнительного штрафа за продолжение пропуска.
Схемы оценок бывают самые разные, но в любом случае, каждому выравниванию может быть сопоставлена некоторая суммарная оценка (вес или счёт), что позволяет количественно оценивать подобие выравниваемых последовательностей (см. также п. 7.2).
Конечно же, желательно иметь схему оценок, присваивающую более высокую оценку биологически правильному выравниванию, учитывающему тот факт, что биологическая молекула имеет эволюционную историю, пространственную структуру, биологическую функцию и другие черты, которые ограничивают "произвол" в варьировании последовательности. Поэтому кроме алгоритмов выравнивания должны быть тщательно продуманы и методы построения системы оценок, которые, в результате, могут быть очень сложными и многофакторными.
Оптимальным называют выравнивание с максимальным счётом, наибольшим числом соответствий и наименьшим количеством различий.
Субоптимальное выравнивание - это условно оптимальное выравнивание, где наивысший счёт находится ниже оптимального уровня.
При оптимальном выравнивании неидентичные знаки и пропуски размещают так, чтобы в столбцах выравнивания было как можно больше идентичных, или подобных знаков.
Оптимальные выравнивания позволяют выявлять эволюционные отношения последовательностей, предоставляя возможно лучшую информацию относительно того, какие знаки последовательностей должны стоять в одних и тех же столбцах выравнивания, а какие являются вставками в одной из последовательностей (или, соответственно, выпадениями в другой). Эта информация необходима для предсказания функций, структур и эволюционных отношений последовательностей по их выравниванию.
Следует подчеркнуть, что, несмотря на то что последовательность редакционных операций получают из оптимального выравнивания, и она, возможно, соответствует реальному эволюционному пути, но невозможно доказать, что это действительно так. Чем больше "редакционное расстояние", тем больше разумных эволюционных путей между двумя последовательностями (см. также п. 7.2).
На рисунке 19 показаны точечные матрицы сравнения одного и того же белка (PAPA_CARPA) сульфгидрильного протеиназного папаина из папайи, с четырьмя гомологами с возрастанием дальности родства между ними:
1) с близким родственником - актинидином из плодов киви (ACTN ACTCH, рисунок 19(a));
2) с более отдалёнными родственниками - человеческим прокатепсином L (CATL_HUMAN, рисунок 19(6));
3) с человеческим катепсином В (CATB_HUMAN, рисунок 19(b));
4) с стафопаином из Staphylococcus aureus (STPA_STAAU, рисунок 19(г)).
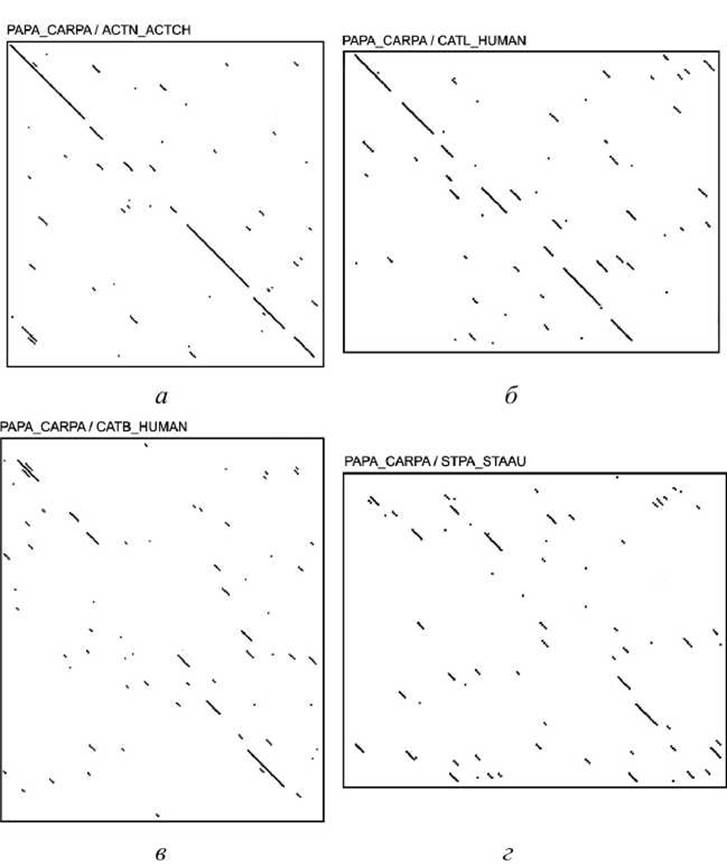
Рисунок 19 - Точечные матрицы выравнивания белка сульфгидрильного протеиназного папаина из папайи с родственными белками
Так как последовательности постепенно расходятся, становится труднее и труднее угадать правильное выравнивание по точечной матрице и для биологически осмысленного выравнивания необходимо привлекать дополнительные данные о структурах белков.
Контрольные вопросы и задания
1. Запишите однобуквенные обозначения нуклеотидов и аминокислот.
2. Что такое генетический код?
3. В чём состоит парадоксальное различие протекания процессов трансляции и фолдинга белка?
4. Анализом каких трёх информационно-управляемых процессов преимущественно занимается биоинформатика?
5. Что называется выравниванием биологических последовательностей?
6. Какие три типа изменений происходят в процессе эволюционного расхождения последовательностей от общего предка?
7. Что такое глобальное выравнивание последовательностей?
8. Что такое локальное выравнивание последовательностей?
9. В чём заключается поиск мотивов совпадения при выравнивании последовательностей?
10. Что такое множественное выравнивание?
11. Что такое точечная матрица сходства и для чего её используют?
12. Как проявляются инверсные и палиндромные последовательности в точечных матрицах сходства?
13. Как проявляются инсерции и делеции в точечных матрицах сходства?
14. Почему с точки зрения биолога поиск локального подобия может дать более значимые и точные результаты, чем оценка выравнивания по всей длине последовательностей?
15. В чём сходство и различие графа и орграфа?
16. Что называют маршрутом в орграфе?
17. Что такое начало (источник) и конец (сток) графа? Какие узлы являются истоками и стоками в графе глобального выравнивания?
18. Что такое оптимальное выравнивание и чем оно отличается от субоптимального?