ОСНОВЫ БИОТЕХНОЛОГИИ МИКРОВОДОРОСЛЕЙ - Д. С. ДВОРЕЦКИЙ - 2015
4. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ПОЛУЧЕНИЯ ПРОДУКТОВ ИЗ МИКРОВОДОРОСЛЕЙ
4.1. Математическое моделирование процесса культивирования микроводорослей
В связи с тем, что экспериментальное исследование процесса культивирования микроводорослей является затратным процессом как с точки зрения ресурсов, так и времени, актуальной задачей является разработка математической модели, способной описывать процессы накопления биомассы клеток микроводорослей, убыли субстрата и накопления липидов.
Процесс культивирования микроводоросли может быть представлен в виде следующей схемы (рис. 22).
Рис. 22. Структурная схема процесса культивирования биомассы: Т - температура; S - вектор концентраций субстратных компонентов; I - интенсивность инсоляции; X - концентрация биомассы микроводорослей; К, μ, Е - кинетические коэффициенты процесса биосинтеза

Протекание стадии интенсивного культивирования биомассы определяется входными параметрами Т, S, I, изменение которых влияет на количество накопленных липидов X, и внутренними Кs, Кi, Кl, μmax, Е, которые зависят от физических свойств среды, вещества и т. д.
При разработке математической модели кинетики роста биомассы микроводоросли и накопления липидов внутри клетки приняты следующие допущения:
Д1. Процесс культивирования биомассы хлореллы состоит из двух периодов: накопления биомассы клеток, в течение которого не происходит образования и накопления липидов; создания стрессовых условий при которых происходит образование и накопление липидов.
Д2. Гидродинамический режим в рабочем объёме фотобиореактора близок к идеальному перемешиванию, поскольку процесс культивирования осуществляется периодическим способом, при интенсивной аэрации газовоздушной смесью. Подвод пузырьков газовоздушной смеси к клетке не затруднён.
Д3. Кислород равномерно распределён по рабочему объёму фотобиореактора и его количества достаточно для осуществления клетками энергетического обмена.
Д4. Освещение в рабочем объёме фотобиореактора осуществляется равномерно.
Д5. Возраст клеток не учитывается при моделировании процесса образования липидов.
Д6. Основным лимитирующим субстратом являются азотосодержащие соли.
Д7. При создании стрессовых условий в питательной среде поддерживается низкая концентрация азотосодержащих солей.
Д8. Процесс культивирования осуществляется в интервале значений pH, оптимальных для накопления биомассы.
Д9. Процессы питания, фотосинтеза, размножения и другие идут одновременно.
Д10. Влияние на скорость роста освещения и концентрации азотосодержащих солей независимо.
Математическая модель кинетики культивирования биомассы микроводоросли Chlorella vulgaris включает в себя следующие уравнения.
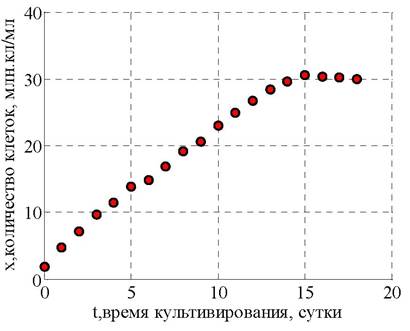
1. Проведённые экспериментальные исследования процесса накопления биомассы микроводорослей (рис. 23) показали, что характер кривой соответствует логистическому уравнению Ферхюльста для ограниченного роста популяции [33]:
![]() (1)
(1)
где X - концентрация биомассы клеток, млн. кл. / мл.; μ - удельная скорость роста, 1/сут; К - ёмкость популяции, млн. кл. / мл.
Рис. 23. Кинетика роста биомассы микроводорослей
2. Процесс убыли субстрата при периодическом культивировании микроводорослей описывается уравнением [34]
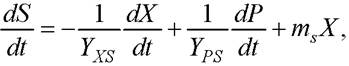 (2)
(2)
где YХS - коэффициент, показывающий количество образующейся биомассы ∆Х при количестве затраченного субстрата ∆S за время ∆t, рассчитывается по экспериментальным данным (млн. кл • л)/(мл • г); YРS - коэффициент, показывающий количество образующихся липидов ∆Р при количестве затраченного субстрата ∆S за время ∆t, рассчитывается по экспериментальным данным; Р - количество липидов, %; ms - коэффициент поддержания жизнедеятельности.
В соответствии с допущением Д7 расходование азотсодержащего субстрата не происходит при накоплении продуктов метаболизма, поэтому второе слагаемое исключаем из уравнения (2). Для неэнергетических субстратов, таких как азот, ms = 0 [34]. Таким образом, уравнение (2) преобразуется к виду (3)
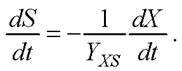 (3)
(3)
3. Количество образующихся липидов Р пропорционально величине накопленной биомассы Х микроводорослей. Для образования липидов необходимо создание стрессовых условий - пониженного содержания субстрата S - азотсодержащей соли, т. е. количество Р должно быть пропорционально 1/ Sr, где r - показатель степени. Концентрация биомассы микроводорослей X достигает максимального значения К, после чего дальнейший прирост прекращается. Можно предположить, что аналогичным образом будет прекращаться рост количества образующихся липидов. Максимально возможное количество липидов будет определяться тогда величиной Рmах. С учётом вышесказанного уравнение для расчёта количества образующихся липидов может быть записано в виде
![]() (4)
(4)
где qP - величина, характеризующая максимальный прирост липидов в единицу времени, 1/сут; Рmах - максимальное количество накопленных липидов, %.
С целью определения коэффициентов, входящих в уравнения (1), (3), (4), был проведён комплекс экспериментальных исследований.
Величина максимальной ёмкости популяции К = 31 млн. кл. / мл определялась из графика, представленного на рис. 23 и соответствовала максимальной достигнутой концентрации клеток биомассы.
Известно [7, 32 - 34], что факторами, оказывающими наиболее сильное влияние на величину удельной скорости роста μ, являются: температура Т, уровень освещённости I, концентрация азотсодержащих солей S, т. е.
μ = μ(Т, 1, 5). (5)
Влияние каждого из факторов рассматривалось при фиксированных и оптимальных значениях других факторов.
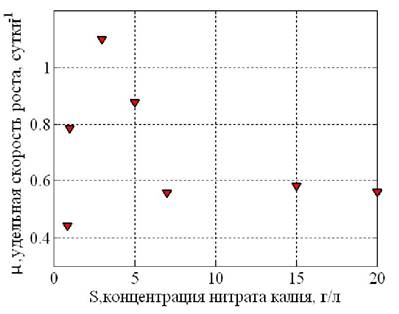
Были проведены экспериментальные исследования по культивированию микроводоросли Chlorella vulgaris в питательных средах при различных значениях концентраций нитрата калия (рис. 24).
Анализ графика, приведённого на рис. 24 позволяет сделать вывод, что процесс ингибирования роста биомассы повышенными концентрациями субстрата S описывается уравнением Эндрюса [4]
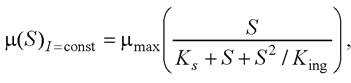 (6)
(6)
где μmax = 1,1 1/сут - максимальная удельная скорость роста микроорганизмов; S - количество субстрата (азотсодержащие соли), г/л; Ks = 1,06 г/л - константа полунасыщения; King = 8,4 - константа ингибирования, г/л, I = const = 5600 лк. Величины μmax, Ks, King определены по графику на рис. 24.
Рис. 24. Зависимость удельной скорости роста μ от количества субстрата S
Влияние уровня освещённости I на кинетику прироста микроводорослей наиболее часто описывается уравнением Михаэлиса-Ментен [35]
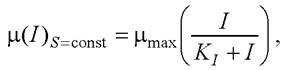 (7)
(7)
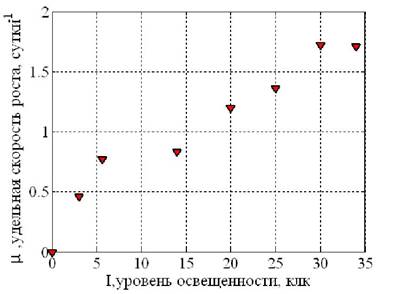
где К1 = 15 000 лк - константа полунасыщения по освещённости, определена по результатам обработки экспериментальных данных при концентрации азотосодержащих солей S = 5 г/л (рис. 25).
Рис. 25. Зависимость удельной скорости роста μ от освещённости I
В процессе культивирования микроводоросли, от температуры Т зависит максимальная удельная скорость роста μmах, входящая в формулы для расчёта μ(S)1=const, μ (l)S=const. Величины Кs и Кing в меньшей степени зависят от температуры Т [34], поэтому уравнение для расчёта максимальной удельной скорости роста μmах было записано в виде степенной зависимости от температуры Т
μmах(Т ) = А0 + А1Т + А2Т 2, (8)
где А0 = -1,3 • 103; А1 = 8,6 ; А2 = -0,01 - коэффициенты, найденные путём решения системы, состоящей из трёх уравнений (9) для температур 300, 303, 308 К.
В соответствии с допущением Д10 принимаем зависимость [34]
μ = 0,5(μ(S)l=const + μ(l)S=const).
Величина Yxs находится как среднее значение, полученное в результате обработки экспериментальных кривых накопления биомассы микроводорослей Х(t) и количества субстратаS(t), по формуле [7]
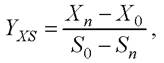 (10)
(10)
где 0, n- первый и последний дни эксперимента Yxs = 6,05 (млн. кл • л)/(мл • г).
Величина удельной скорости биосинтеза продуктов qр рассчитывалась по аналогии с формулой для расчёта удельной скорости роста клеток [7] по формуле
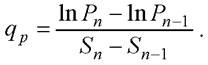 (11)
(11)
Величины qр = 1,5; Рmах = 32% и r = 2 были определены в результате обработки экспериментальных данных по кинетике накопления липидов.
Решение системы обыкновенных дифференциальных уравнений (1), (3), (4), (5) осуществлялось методом Рунге-Кутта 4 порядка [35] в среде Matlab [36]. Начальные условия при t = 0:
Х(0) = 2, S(0) = 5, Р(0) = 4. (12)
Результаты решения представлены на рис. 26 - 28.
Рис. 26. Количество клеток биомассы, млн. кл. / мл
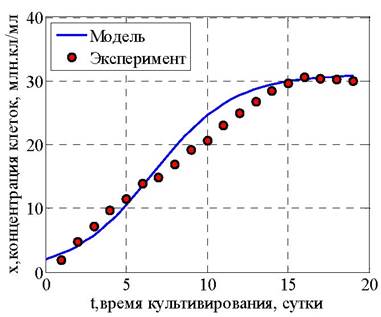
Рис. 27. Количество субстрата, г/л
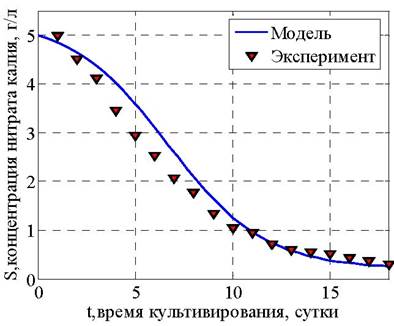
Рис. 28. Количество липидов, % масс.
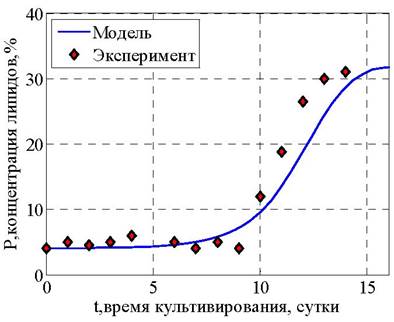
Анализ полученных результатов позволяет сделать заключение, что максимальная величина прироста биомассы микроводорослей и накопления внутриклеточных липидов обеспечивается в период до 15 суток, после чего стадию биосинтеза целесообразно прекратить.
4.2. Математическое моделирование процесса разрушения клеток
Разрушение клеток обычно описывают кинетической моделью первого порядка, как, например, описывал Хезерингтон и другие [37] для дрожжевой клетки, разрушенной для извлечения белков. Похожая кинетическая модель первого порядка используется для описания разрушения клеток микроводорослей с помощью ультразвука или гомогенизации высоким давлением (ГВД):
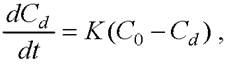 (13)
(13)
где Сd - число клеток, которые были разрушены в единице объёма за время 1 (клеток/мм3); С0 - количество неповреждённых клеток, первоначально присутствующих в культуре на единицу объёма или начальная концентрация клеток культуры (клеток/мм3); t - длительность разрушения в эксперименте; К - константа скорости разрушения. При ультразвуковом разрушении t является временем действия ультразвука (с); К - константой скорости разрушения ультразвуком (1/с). Для ГВД, t - количество проходов через ГВД-клапан, К - константа скорости разрушения ГВД (1/проход).
Начальное условие может быть записано в виде
Сd (0) = 0. (14)
Решая уравнение (13) с начальным условием (14), получим Сd = С0(1 - е-Кt). (15)
Далее осуществляется переход к безразмерным переменным Сd = Со — С (16)
где С - количество интактных (целых) клеток, присутствующих в культуре на единицу объёма в момент времени 1 (клеток/мм3).
Подставляя (16) в (15), получаем С0 - С = С0(1 - е-Кt). (17)
В безразмерных переменных уравнение (17) можно записать в виде D = (1 - е-Кθ), (18)
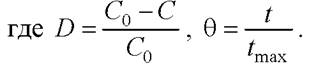
В уравнении (18) D - безразмерная концентрация клеток микроводорослей культуры; К - безразмерная постоянная скорости разрушения;
θ - безразмерное время; tmax - максимальная продолжительность эксперимента, при которой проводилось разрушение (25 мин для обработки ультразвуком, 5 проходов для ГВД).
Величина D характеризует часть неповреждённых клеток культуры, которая была подвергнута процессу разрушения в течение времени t и может быть понята как степень разрыва. Безразмерная постоянная скорости разрушения K характеризует эффективность процесса разрушения клеток микроводорослей. Более высокое значение K указывает на более быстрое разрушение клеток.
4.3. Математические модели процесса экстракции
Процесс экстракции из растительного материала поясняется рис. 29 [22]. Процесс экстракции может быть разбит на несколько этапов.
Рис. 29. Схема процесса экстракции липидов из клетки
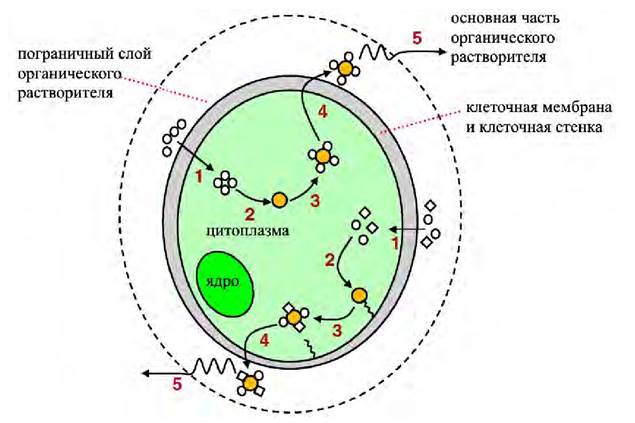
Этап 1. Смесь неполярного и полярного органических растворителей проникает через клеточную мембрану в цитоплазму.
Этап 2. Смесь взаимодействует с липидным комплексом. Во время этого взаимодействия неполярный органический растворитель окружает липидный комплекс и образует ван-дер-ваальсово взаимодействие с нейтральными липидами в комплексе, в то время как полярный органический растворитель также окружает липидный комплекс и образует водородные связи с полярными липидами в комплексе. Водородные связи достаточно сильны, чтобы заместить связывание липидов в липид-белковых ассоциациях клеточной мембраной.
Этап 3. Формируется комплекс органический растворитель-липиды и отделяется от клеточной мембраны.
Этап 4. Комплекс органический растворитель-липиды диффундирует через мембрану клетки.
Этап 5. Липиды диффундируют через статическую плёнку органического растворителя, окружающую клетку, в объём органического растворителя.
При этом выделение липидов в процессе экстракции органическим растворителем из биомассы микроводорослей описывается кинетическим уравнением первого порядка [22] mе = m0(1- e-kt), (19)
где me - количество липидов, извлечённых органическим растворителем за время t (г липидов/г сушёной биомассы микроводорослей); m0 - объём липидов, изначально присутствующий в клетках (г липидов/г сухой биомассы микроводорослей); k - коэффициент массопередачи липидов из клеток микроводорослей в органический растворитель (1/с); t - время экстракции (с).
Схожесть уравнений (19) и (15) указывает на одинаковый подход к описанию процессов разрушения клеток и извлечения липидов.
Согласно [38] экстракция липидов из клеток может быть описана с помощью основного уравнения массопередачи
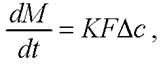 (20)
(20)
где К - коэффициент массопередачи, показывающий количество вещества, переносимого через единицу поверхности в единицу времени при величине движущей силы (разности рабочей и равновесной концентраций), равной единице,![]() - количество вещества, переходящего из одной фазы в другую в единицу веремени, моль/с; F - поверхность контакта фаз, м2; ∆с - движущая сила процесса массообмена - разность рабочей и равновесной концентраций, выраженная в соответствующих единицах, м3/м3.
- количество вещества, переходящего из одной фазы в другую в единицу веремени, моль/с; F - поверхность контакта фаз, м2; ∆с - движущая сила процесса массообмена - разность рабочей и равновесной концентраций, выраженная в соответствующих единицах, м3/м3.
В общем случае процесс экстракции может складываться из трёх составляющих:
- «внутренняя» диффузия, характеризующая перенос вещества внутри клетки, от ядра к поверхности (количественно оценивается величиной коэффициента внутренней диффузии Dвн);
- перенос вещества в пределах непосредственного диффузионного пограничного слоя вокруг клетки от её поверхности к границе пограничного слоя (количественно оценивается величиной коэффициента D);
- перенос вещества движущимся экстрагентом в результате конвективной диффузии от пограничного слоя в раствор (количественно оценивается величиной коэффициента массоотдачи β).
Поэтому коэффициент массопередачи К может быть рассчитан как величина, обратная суммарному сопротивлению переноса вещества из ядра одной фазы (внутриклеточное пространство) в ядро другой фазы (раствор), т. е.
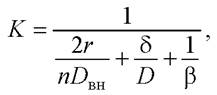 (21)
(21)
где 2r - диаметр клетки; n - коэффициент; Dвн - коэффициент внутренней диффузии; D - коэффициент молекулярной диффузии; δ - толщина диффузионного пограничного слоя; β - коэффициент масоотдачи.
Формула (21) применима, когда жидкая фаза перемещается с небольшой скоростью (например, осуществляется перемешивание в аппарате с мешалкой), соответственно, присутствуют все три составляющих.
В случае, если жидкая фаза неподвижна, вещество из ядра клетки к поверхности и от поверхности далее в раствор будет перемещаться исключительно диффузией, в таком случае «пограничный слой» фактически займёт весь объём реактора. Формула (21) тогда запишется в следующем виде:
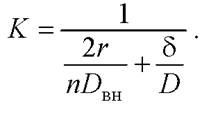 (22)
(22)
В случае, если жидкая фаза перемещается с большой скоростью (интенсивное перемешивание), пограничный слой вокруг клетки будет отсутствовать, внешняя массоотдача не будет оказывать влияние на процесс, т. е. фактически будет достигаться идеальное перемешивание. В таком случае скорость процесса определяется исключительно внутренней диффузией молекул внутри клетки:
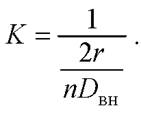 (23)
(23)
Для выражения величины коэффициента внутренней диффузии в клетках в уравнение Эйнштейна для свободной диффузии предлагается вводить поправочный коэффициент В, учитывающий все осложнения процесса:
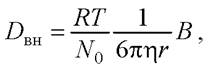 (24)
(24)
где R - универсальная газовая постоянная, Дж/моль • К; Т - абсолютная температура, К; N0- число Авоградро; ɳ - вязкость в Н/(с • м2); r - радиус клеток, м.
Величина коэффициента диффузии D может быть найдена по уравнению Аррениуса
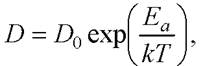 (25)
(25)
где D0 - предэкспоненциальный множитель, численно равный коэффициенту диффузии при бесконечно большой температуре; Еа - энергия активации.
Существует несколько способов осуществления экстрагирования [7]: экстрагирование с перемешиванием, экстрагирование в неподвижном слое, экстрагирование одно- и многоступенчатое, прямоточное и противоточное.
Экстрагирование с перемешиванием является наиболее простым способом экстрагирования. В аппарат с мешалкой загружается твёрдая фаза (биомасса после сгущения или отделения на фильтре) и жидкая фаза (экстрагент). Процесс далее протекает при перемешивании.
Концентрация извлекаемого вещества в экстрагенте изменяется во времени в соответствии с уравнением
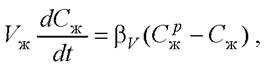 (26)
(26)
где Vж - объём жидкой фазы и аппарате; Сж - концентрация растворённого вещества в экстракте в момент времени t; βV - коэффициент массоотдачи жидкость-твёрдое тело в пересчёте на объём жидкой фазы.
Величина Сpж в формуле обозначает концентрацию растворённого вещества в жидкости, равновесную с его содержанием в твёрдой фазе СТ. Предполагается, что связь между ними определяется законом Рауля
![]() (27)
(27)
где γжт - коэффициент распределения, показывающий, во сколько раз концентрация растворённого вещества в жидкости при равновесии (отсутствия дальнейшего растворения) больше, чем его концентрация в твёрдой фазе. Обычно экстрагент подбирается таким образом, что растворимость в нём извлекаемого вещества значительно больше, чем в твёрдой фазе (т. е. γжт >> 1).
С другой стороны, концентрация растворённого вещества в твёрдой фазе соответствует уравнению
![]()
или
![]() (28)
(28)
где Vт - объём твёрдой фазы в аппарате.
Решая уравнения (27) и (28), можно определить, как меняется концентрация растворённого вещества в жидкой и твёрдой фазах.
На рисунке 30 показано, что концентрация вещества в твёрдой фазе резко падает от начального значения Ст0 до равновесного Стр. Концентрация же в жидкой фазе увеличивается не так значительно: от Сж0 = 0 до равновесного Сжр, но при этом концентрация в жидкости Сж после некоторого момента времени, начинает превышать концентрацию в твёрдой фазе, т. е. Сж > Ст. Казалось бы, при этом растворённое вещество должно переходить из жидкости обратно в твёрдую фазу, но реально извлечение идёт, пока не установятся равновесные значения Стр и Сжр. Если же сравнивать между собой значения Ст и Сж / γжт = Ст*, то график выглядит по-другому (рис. 31).
Рис. 30. Изменение в процессе экстрагирования концентраций растворённого вещества в твёрдой (1) и жидкой (2) фазах
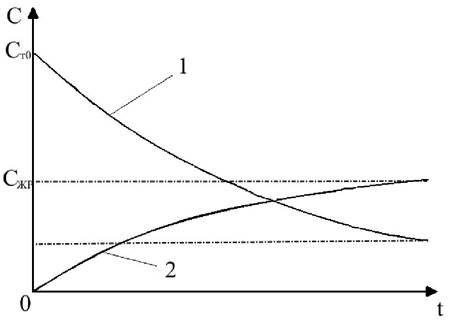
Рис. 31. Изменение движущей силы процесса экстрагирования
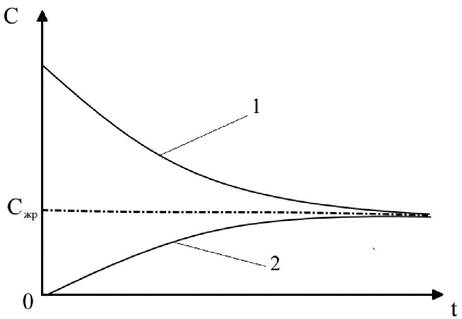
Этот график показывает, что к концу процесса движущая сила массоотдачи становится равной нулю.
При равновесии во всех случаях должно быть справедливо уравнение
![]() (29)
(29)
С другой стороны, в равновесном состоянии сумма количеств вещества, растворённого в твёрдой и жидкой фазе, должна быть равна величине, имевшей место в начале процесса экстрагирования:
![]() (30)
(30)
Решая эти уравнения вместе, получаем
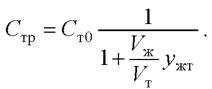 (31)
(31)
Из этого соотношения видно, что концентрация растворённого вещества в биомассе после однократного экстрагирования существенно меньше, чем перед ним. Эта величина тем меньше, чем больше коэффициент распределения γжт и чем больше соотношение объёмов жидкости и твёрдой фазы Vж / Vт.
Так же видно, что на конечную величину концентрации не влияет коэффициент массоотдачи βv: он лишь ускоряет или замедляет процесс экстрагирования при одинаковом итоговом результате.