Принципы структурной организации белков - Г. Шульц 1982
Статистическая механика перехода спираль - клубок
Вероятность данной конформации остатка
Если пренебречь растворителем и всеми взаимодействиями остаток — остаток, функция распределения выражается произведением статистических весов отдельных остатков. Эти статистические веса можно разбить на веса для областей aR, aLи ε. Если пренебречь всеми взаимодействиями между остатками, то энергию можно разделить на вклады отдельных остатков и разложить интеграл на множители:
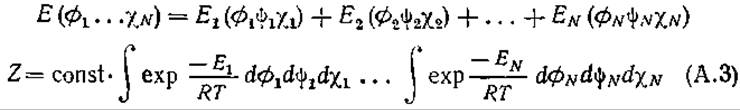
Полученные интегралы отдельных остатков можно аппроксимировать путем сведения пределов интегрирования к тем областям, в которых отсутствуют стерические напряжения, т. е. где значение Ei не слишком велико. Как видно из рис. 2.3, б, имеются области правой и левой а-спиралей, а также вытянутой цепи, обозначенные aR, aL и ε.
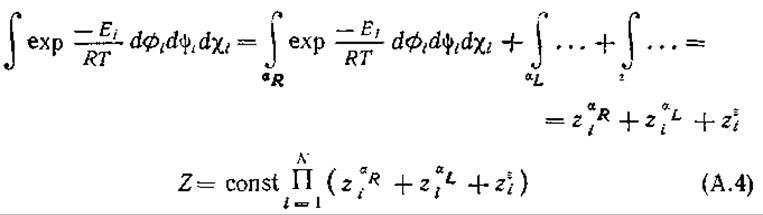
Здесь 
— статистические веса соответственно областей aR, aL и ε. Они специфичны для данного типа остатка, т. е. 
представляют собой вероятности того, что фрагмент остова, отвечающий остатку і, примет какую-либо из конформации соответственно в областях aR, aL и ε. Другими словами, величины 
отражают склонность остатка находиться в конформации aR, aL, ε. Эти вероятности зависят от энергии Ei в этой области и о размера области. Таким образом, при сравнении вероятностей or и в более низкая энергия для aR (лучшее связывание) вполне может быть компенсирована большей величиной области для є (рис. 2.3).
Эмпирические статистические веса можно получить из наблюдаемых частот встречаемости. В принципе эти склонности можно рассчитать для каждого типа остатка по энергетическим картам, подобным приведенной на рис. 2.5. Однако эти карты следует расширить с тем, чтобы учесть зависимость от конформации боковой цепи. Кроме того, для получения разумных результатов нужно принять во внимание растворитель, что, однако, сделать достаточно сложно.
С другой стороны, близкие значения с этими вероятностями 
можно получить путем приравнивания их частотам встречаемости состоянии aR, aL, ε рассматриваемого типа остатка в глобулярных белках известной структуры. Эта процедура принята в большинстве методов предсказания.
Карта общей эмпирической энергии получена из частот встречаемости. Используя аппроксимацию уравнения (А.З), из наблюдаемых в глобулярном белке углов (—, ψ) всех типов остатков можно получить карту общей эмпирической энергии Е(—, ψ). Для этой цели частоты встречаемости остатков (безотносительно к типу остатка), найденные в данной (—, ψ)-области (рис. 2.4), приравнивают к статистическим весам 
в этой области. Отсюда статистические веса, а следовательно, и Е можно выразить как функцию углов (—, ψ). Эмпирическая энергия Е(—, ψ) достаточно хорошо согласуется с рассчитанной (рис. 2.5) [786].