Принципы структурной организации белков - Г. Шульц 1982
Статистическая механика перехода спираль - клубок
Модель Зимма - Брэгга для перехода спираль - клубок
Матричное представление
Функция распределения в матричной форме. Крамере и Ванье [790] предложили записать уравнение (А.6) в компактней матричной форме, упрощающей расчет Z.
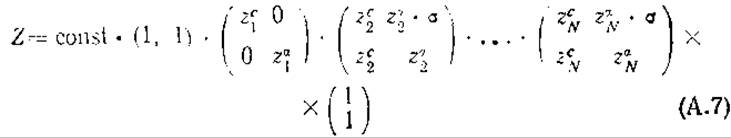
Проверим соответствие этого выражения уравнению (А.6) при малых N:
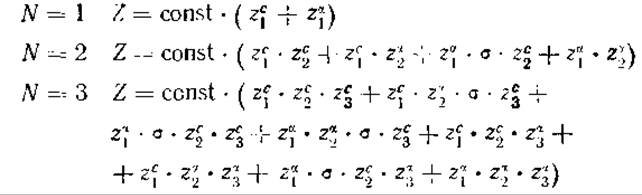
Эти соотношения можно распространить и на большие значения N.
Простой случай гомополимера удовлетворительно описывается матрицей N-гo порядка в терминах собственных значений. Если применить уравнение (А.7) к гомополимерам, то все величины zia, как и величины zci, будут одинаковы. Для дальнейшего упрощения относительные статистические веса s можно выразить как
![]()
Будем считать (zсі)N за постоянную, которую опустим, поскольку интерес представляет только изменение Z при переходе спираль — клубок, а не ее абсолютное значение.
![]()
Путем диагонализации матрицы это можно свести к выражению:
![]()
При
![]()

то есть Z можно в явном виде выразить как функцию собственных значений.
![]()
Поскольку λ1 > 1 > λ2 при всех s и σ, то для больших N статистическую сумму можно аппроксимировать как
![]()