Основы биоинформатики - Огурцов А.Н. 2013

Методы биоинформационного анализа
Алгоритмы выравнивания последовательностей
Алгоритм динамического программирования

Алгоритм глобального оптимального выравнивания двух последовательностей, дающий максимальное количество баллов (максимальный вес (счёт, score)) основан на математическом методе, называемом динамическим программированием.

Основное достоинство этого метода состоит в том, что он гарантирует глобальный оптимум: наилучший результат выравнивания при заданном наборе параметров - матрице замещений и штрафных значениях для пропусков - без каких-либо приближений.

Основной недостаток метода состоит в том, что многие выравнивания двух данных последовательностей могут привести к оптимальному числу баллов, при этом совершенно не обязательно, что хотя бы одно из них имеет отношение к биологически корректному выравниванию (имеет биологический смысл). Например, при сравнении последовательностей а- и ß-цепей гемоглобина цыпленка В. Фитч и Т. Смит (W. Fitch и Т. Smith) нашли 17 выравниваний, каждое давало одинаковое оптимальное число баллов, из которых корректным, (используя дополнительную информацию о пространственной структуре белков) оказалось только одно. И вообще, оказалось, что для этой задачи существует 1317 выравниваний, которые дают число баллов в пределах 5% от оптимума.

Есть ещё один недостаток - время, требуемое для выравнивания двух последовательностей длиной п и m пропорционально размеру редактируемой матрицы, то есть, пропорционально произведению m х n. Вычислительную сложность алгоритма обозначают O(f). Поскольку обычно n и m одного порядка, про алгоритм говорят, что он требует O(n²) времени (или памяти). В области анализа биологических последовательностей обычными компьютерами (а не суперкомпьютерами) алгоритмы O(n²) дают удовлетворительные результаты, а вот алгоритмы O(n³⁾ возможно применять только для очень коротких последовательностей.

Таким образом, метод динамического программирования будет слишком медленным при поиске соответствия для пробной последовательности в полной базе данных последовательностей, и ещё меньше он подходит для выравниваний "все-против-всех". Проблема поиска в базе данных - это на самом деле проблема поиска соответствия интересующей нас последовательности с очень длинной последовательностью, длина которой равна всей базе данных.

Схема, содержащая все возможные выравнивания, может быть построена в виде матрицы, подобной той, которая используется для изображения точечной матрицы сходства. Элементы одной последовательности (нуклеотиды или аминокислоты) индексируют строки, а элементы другой последовательности - столбцы. Любой путь по матрице, начинающийся в левом верхнем углу и заканчивающийся в правом нижнем, соответствует одному выравниванию (см. рисунок 17). Задача состоит в том, чтобы найти путь, имеющий максимальный счёт, и трудность состоит в том, что таких путей нужно рассмотреть очень много.

Для понимания основной идеи динамического программирования рассмотрим элементарный пример "перемещения" по графу 5x5 из начальной точки (0,0) в конечную точку (4,4) (рисунок 47(a)).

Существует 6 путей из начальной точки (0,0) в точку "А" (рисунок 47(6)). Исходя из симметрии, существует также и 6 путей из точки "А" в конечную точку (4,4), а общее число путей из начала в конец, проходящих через точку "А", равно 36.

Пусть, далее, мы присвоили цены отдельным этапам. Вопрос заключается в том, нужно ли нам проверять все 36 путей для нахождения оптимального, который проходит из начала в конец через точку "А"?

Оказывается не нужно, поскольку выбор оптимального пути из точки "А" в конец не зависит от выбора пути из начала в точку "А".

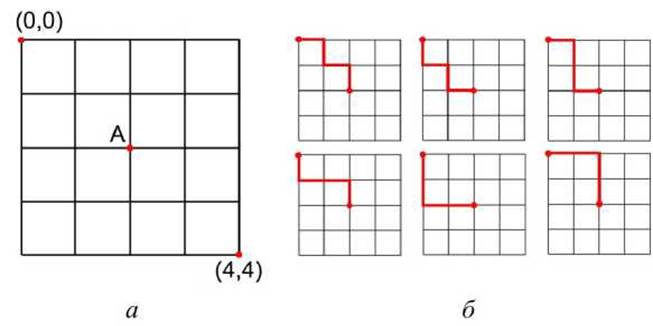
Рисунок 47 - Модельный граф: а - схема; б - пути из точки (0,0) в точку А

Если мы определяем оптимальный из 6 путей, ведущих от начальной точки в точку "А", а также оптимальный из путей от "А" к концу, то оптимальный путь от начала к концу, проходящий через "А", будет определяться как оптимальный путь от начала к "А" и следующий за ним оптимальный путь от "А" к конечной точке.

В этом случае нужно рассматривать уже не более 12 путей, проходящих через точку "А" - 6 путей от точки (0,0) до "А", продолжающихся самым оптимальным из путей от "А" до конца; плюс ещё 6 путей от "А" до конца, продолжающих единственный оптимальный путь от начала к "А".

В этом и заключается преимущество метода динамического программирования - задача систематически разделяется на всё более мелкие части (рисунок 48). И тем самым сокращается объём необходимых вычислений.

Алгоритм глобального выравнивания двух биологических последовательностей методом динамического программирования был впервые предложен Солом Нидлманом и Кристианом Вуншем (Saul В. Needleman и Christian D. Wunsch).

Для идентификации локального совпадения подобный алгоритм был впервые использован Темплем Смитом и Михаэлем Уотерманом (Temple F. Smith и Michael S. Waterman).

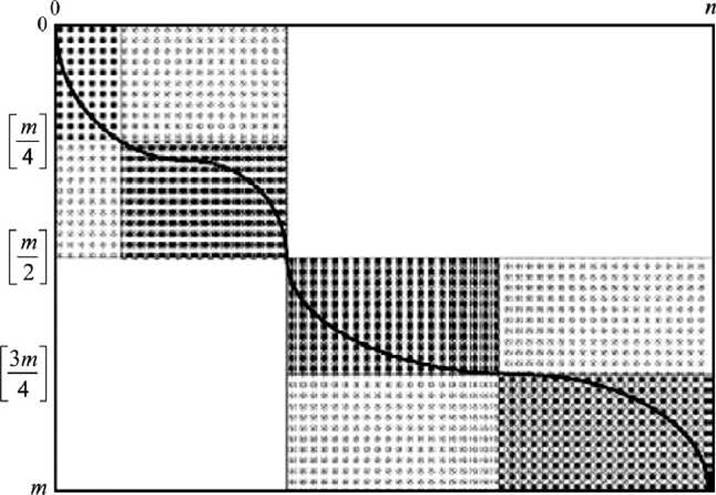
Рисунок 48 - Разбиение задачи оптимального выравнивания на подпрограммы