Основы биоинформатики - Огурцов А.Н. 2013

Методы биоинформационного анализа
Алгоритмы выравнивания последовательностей
Алгоритм глобального выравнивания

Алгоритм глобального выравнивания Нидлмена-Вунша методом динамического программирования заключается в построении на данном этапе оптимального выравнивания, используя полученные на предыдущих этапах оптимальные выравнивания начальных фрагментов исходных последовательностей.

Для двух выравниваемых последовательностей х и у с элементами x_i (0 < і < n) и у_j (0 < j < m) мы строим матрицу F.

Элемент F(i, j) этой матрицы содержит вес (счёт, score) наилучшего выравнивания начальных фрагментов х_1...i (длиной і) и у_1...j(длиной j) последовательностей х и у, соответственно. Матрицу F мы строим рекурсивно. Начинаем с того, что присваиваем начальной точке нулевой вес F(0,0) = 0. Далее мы заполняем матрицу в порядке возрастания обоих индексов, то есть с верхнего левого угла к нижнему правому. Если уже известны F(i - 1, j - 1), F(i - 1, j) и F(i, j - 1), то можно вычислить F(i, j).

Возможны три варианта получения веса F(i, j) в соответствии с тремя возможными вариантами выравнивания, представленными на рисунке 49.

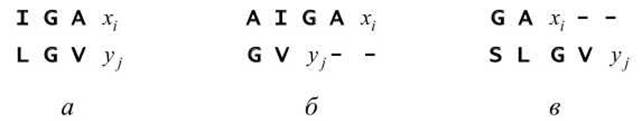
Рисунок 49 - Три способа продолжения выравнивания до точки а - элемент х_i - выровнен с у_j; б - элементу х_i сопоставлен пропуск (gap); в - элементу уj сопоставлен пропуск

Элемент xi одной последовательности может быть выровнен с элементом уj второй последовательности (рисунок 49(a)), и тогда к значению веса F(i - 1, j - 1) добавляем очки за выравнивание s(x_i, y_j) (например, из матрицы BLOSUM)

F(i, j) = F(i - 1, у - 1) + s(x_i, y_j).

Если же элементу хi одной последовательности сопоставлен пропуск (gap) во второй последовательности (рисунок 49(6)), то за это "начисляется" штраф d

F(i, j) = F(i -1, j) - d.

В случае, когда элементу у_j сопоставлен пропуск в последовательности x (рисунок 49(b)), также "начисляется" штраф

F(i, j) = F(i, j - 1) - d.

Наибольший вес выравнивания двух фрагментов последовательностей x_1...i (длиной і) и y_1...j (длиной j) определяется как максимум этих трёх вариантов

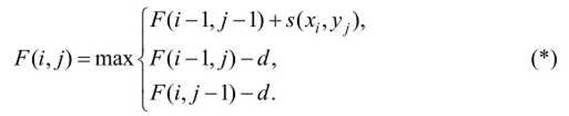
Такую рекурсивную процедуру повторяем, последовательно увеличивая номер строки j (а внутри строки - последовательно увеличивая номер столбца і), до тех пор, пока не будет заполнена вся матрица F(i, j).

Рассмотрим "квадрат", состоящий из четырёх соседних ячеек матрицы (рисунок 50).

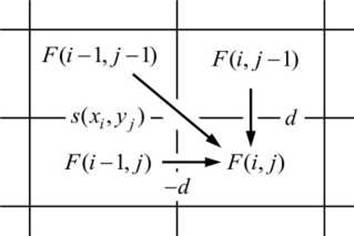
Рисунок 50 - Три варианта получения веса F(i, j)

Каждое последующее значение F(i, j) в правом нижнем углу каждого такого "квадрата" из четырёх ячеек определяется из одной из оставшихся трёх ячеек (показано стрелками на рисунке 50).

При заполнении матрицы F одновременно с вычислением значений F(i, j) необходимо запоминать, по какому из трёх "путей" (из какой клетки на рисунке 50) было получено это конкретное значение F(i, j).

Такое запоминание впоследствии, после заполнения всей матрицы, нужно для восстановления "маршрута" выборов.

Прежде чем закончить описание алгоритма необходимо определить граничные условия - процедуру заполнения ячеек верхней строки (J = 0) и левой колонки (і = 0).

Поскольку вдоль верхней строки, где (j = 0), получение значений F(i, 0) при движении слева направо (горизонтальная стрелка на рисунке 50) соответствует вставкам пропусков в последовательность у, то устанавливаем

F(i, 0) = -d.

Аналогично вдоль левой колонки с (i = 0)

F(0, j) = -d.

Рассмотрим последовательность заполнения матрицы динамического программирования на примере глобального выравнивания двух последовательностей

с использованием матрицы замен BLOSUM50 и значения величины штрафа d = 8.

Сначала, в соответствии с правилом заполнения верхней строки (у = 0) и левой колонки (i = 0), заполняем соответствующие ячейки матрицы динамического программирования нарастающим штрафом (рисунок 51) и отмечаем стрелками "путь" заполнения соответствующей ячейки.

Затем начинаем заполнять строку с j = 1. Для ячейки (1,1), то есть для пары аминокислот (Н,Р) вычисляем три возможные варианта, в соответствии с алгоритмом (*) (стр. 177) и отмечаем стрелкой-указателем, из какой ячейки была заполнена данная ячейка

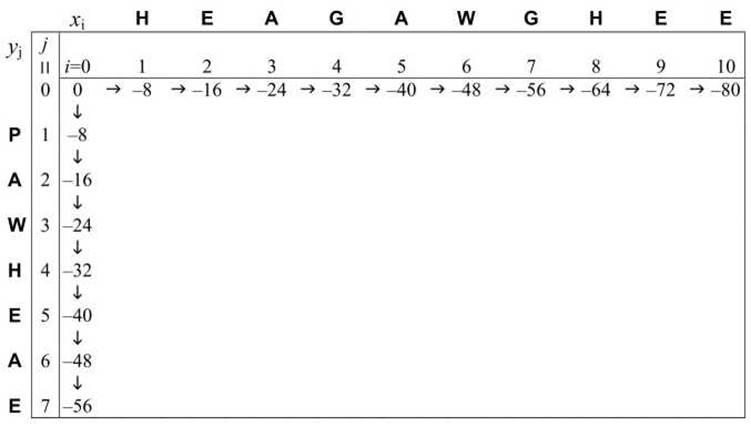
Рисунок 51 - Заполнение верхней строки и левой колонки матрицы

Для ячейки (1,1) максимальным будет значение (-2) при переходе из ячейки (0,0), поэтому отмечаем стрелкой (↘) переход из ячейки (0,0) в ячейку (1,1) (рисунок 52).

Продолжаем заполнять строку с j = 1. Для ячейки (2,1) или (Е,Р) матрицы динамического программирования вычисляем три возможные варианта, в соответствии с алгоритмом (*) (стр. 177)

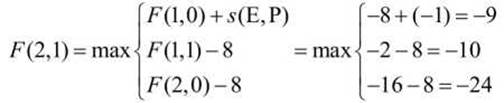
и отмечаем соответствующий переход стрелкой (↘) (рисунок 52). Для ячейки (3,1) или (А, Р) матрицы

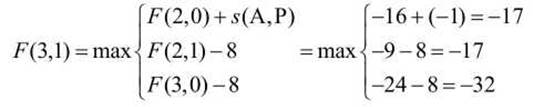
имеется два одинаковых максимума (-17), соответственно отмечаем два варианта перехода к ячейке (3,1) из ячеек (2,0) и (2,1) (рисунок 52).

Рисунок 52 - Заполнение строки с j = 1

Далее для оставшихся ячеек строки j = 1:

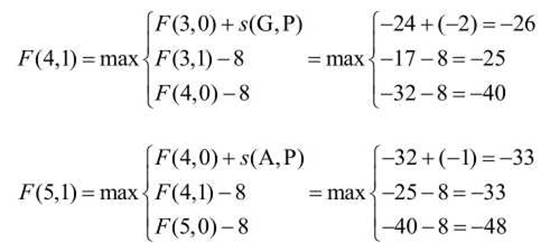
Аналогично, заполняем оставшиеся ячейки матрицы (рисунок 53).

Рисунок 53 - Заполнение матрицы динамического программирования

Значение правой нижней ячейки матрицы F(n,m) по определению является наилучшим весом выравнивания двух последовательностей х_1...i и у_х...j. Для построения самого выравнивания необходимо восстановить последовательность выборов, которая и привела от начальной точки (0,0) к финальной точке (n,m).

Процедура восстановления выборов называется процедурой обратного прохода (traceback procedure). Она осуществляется построением выравнивания с конца, от правой нижней ячейки матрицы с координатами (n,m), следуя тем указателям шагов, которые были получены при построении матрицы.

На рисунке 54 стрелками показаны указатели для обратного прохода.

Рисунок 54 - Схема обратного прохода

На каждом шаге процедуры обратного прохода мы движемся от текущей ячейки (i,j) "обратно" к одной из ячеек (i - 1, j - 1), (i - 1, j), (i, j - 1) из которых и было вычислено значение веса F(i, j).

При этом мы строим граф обратного прохода и, одновременно, записываем выравниваемые строки, добавляя слева к текущему выравниванию пару символов:

- если вес был получен из ячейки (і - 1, j - 1) (диагональная стрелка);

- если вес был получен из ячейки (i - 1, j) (горизонтальная стрелка);

- если вес был получен из ячейки (i, j - 1) (вертикальная стрелка).

В конце выравнивания мы достигаем левого верхнего угла матрицы (0,0).

Для нашего примера оказываются возможными три варианта выравнивания с одинаковым весом 1:

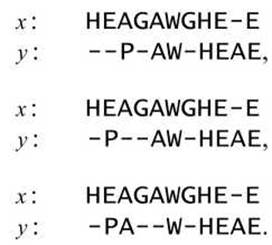
Существование нескольких оптимальных выравниваний с одинаковым весом (счётом) проявляется в виде "развилок" в графе обратного прохода в матрице динамического программирования. Развилка появляется в том случае, если процедура обратного прохода, восстанавливающая оптимальный путь, достигает в матрице динамического программирования ячейки (i, j), оптимальное значение которой F(i, j) было получено из более чем одной "родительской" ячейки. Это и порождает различные пути через матрицу динамического программирования и, следовательно, различные оптимальные выравнивания.

Рассмотрим ещё два характерных примера, иллюстрирующих возможности алгоритма глобального выравнивания.

Построим глобальное выравнивание двух последовательностей ДНК: gaattc и gatta, назначая (+2) очка за совпадение, (-1) за несовпадение и линейный штраф за пропуски d = 2.

Повторяя все шаги алгоритма из предыдущего примера, получаем матрицу динамического программирования с указателями обратного прохода (рисунок 55).

Рисунок 55 - Матрица выравнивания последовательностей gaattc и gatta

Соответственно, возможны два оптимальных выравнивания со счётом 5:

Второй пример. Найдём оптимальное глобальное выравнивание нуклеотидных последовательностей tacgagtacga и actgacgactgac с условием, что нуклеотиды д, показанные жирным шрифтом, должны быть выровнены друг относительно друга. Очки: за совпадение (+2), за несовпадение (-1), за пропуски пропорциональный штраф d = -2.

Легко видеть, что средние нуклеотиды g делят каждую последовательность на две идентичные подпоследовательности. Следовательно, если мы найдём оптимальное выравнивание подпоследовательностей tacga и actgac, то оптимальное глобальное выравнивание, удовлетворяющее условию выровненности средних нуклеотидов д, будет сцепкой этих двух "подвыравниваний" с парой выровненных нуклеотидов g между ними. Поэтому сначала вычисляем матрицу подвыравнивания (рисунок 56) и методом обратного прохода строим само подвыравнивание.

Рисунок 56 - Матрица выравнивания последовательностей tacga и actgac Выравнивание последовательностей tacga и actgac

а его счёт равен 2. Искомое глобальное выравнивание имеет вид

а его счёт S = 2 + s(g,g) + 2 = 2 + 2 + 2 = 6.

Оказывается, что это "условное" (с условием выровненности средних д) оптимальное выравнивание совпадает с одним из двух "безусловных" оптимальных глобальных выравниваний заданных последовательностей tacgagtacga и actgacgactgac. Второе оптимальное глобальное выравнивание (с тем же счётом, равным 6) имеет следующий вид

В этом выравнивании два нуклеотида g не выровнены друг относительно друга. Однако потеря положительного счёта за совпадение компенсирована уменьшением числа пропусков.