Основы биоинформатики - Огурцов А.Н. 2013

Методы биоинформационного анализа
Алгоритмы выравнивания последовательностей
Алгоритм локального выравнивания

Алгоритм Смита-Уотермана используют в случае, когда необходимо найти оптимальное выравнивание подпоследовательностей (subsequences) исходных последовательностей х и у, например, когда производится поиск общих доменов у белков.

Локальное выравнивание также является эффективным способом обнаружения сходства при сравнении сильно дивергировавших последовательностей.

Наилучшим локальным выравниванием называется выравнивание подпоследовательностей х и у с самым большим весом.

В целом алгоритм локального выравнивания подобен алгоритму глобального выравнивания, но в нём существуют два отличия.

Первое отличие - для получения значения веса для каждого элемента матрицы динамического программирования добавлена возможность присвоения нулевого веса F(i,j) = 0 в случае, если все остальные варианты выбора дают отрицательные значения

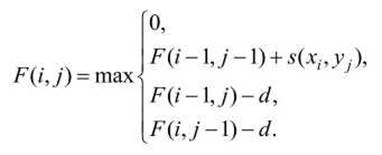
Если наилучшее выравнивание на данном этапе имеет отрицательный вес, то лучше начать новое выравнивание, чем продолжать старое. Всякий раз, когда наилучший вес в ячейке матрицы оказывается отрицательным, в ячейку записывается 0 и ставится метка, что отсюда дальше пути нет, и что начинается новое выравнивание. Поэтому в матрице динамического программирования при локальном выравнивании не бывает отрицательных значений.

Вследствие добавления нового "нулевого" выбора, элементы верхней строки и левого столбца в данном алгоритме также приравниваются нулю, а не -id и -jd, как при глобальном выравнивании.

В результате любая подпоследовательность может "скользить" вдоль другой перед началом выравнивания без прибавления штрафов за вставки пропусков (делеции) оставленные позади.

Второе отличие - выравнивание может закончиться в любом месте таблицы, а не только в правом нижнем углу, как в случае глобального выравнивания. Таким образом, вместо F(n, m) наилучшим весом при локальном выравнивании может быть наибольшее значение F(i, j) в матрице, и процедуру обратного прохода нужно начинать именно с этого места. На рисунке 57 показан пример нахождения локального выравнивания

тех же последовательностей, для которых на рисунке 53 было найдено глобальное выравнивание. В данном случае локальное выравнивание оказалось подмножеством глобального выравнивания. Однако это не всегда так.

В настоящее время в программах осуществляющих поиск локальных совпадения используют модифицированные алгоритмы Смита- Уотермана, в которых используются аффинные функции штрафов за разрывы.

Рисунок 57 - Локальное выравнивание методом Смита-Уотермана